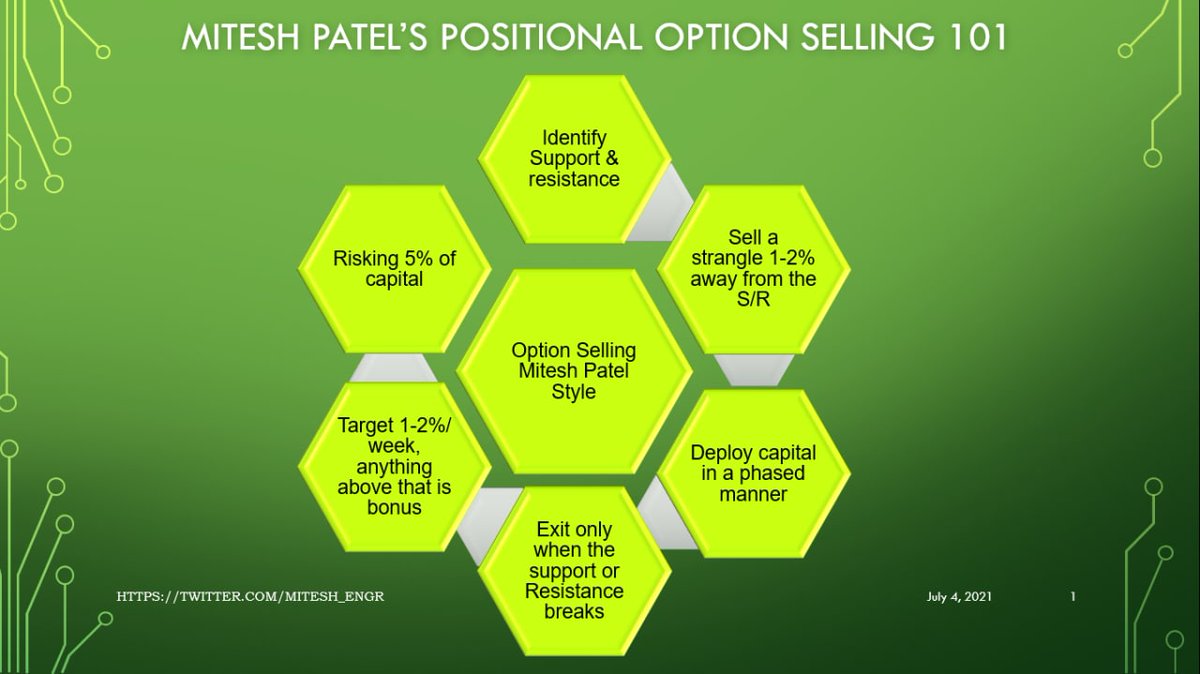
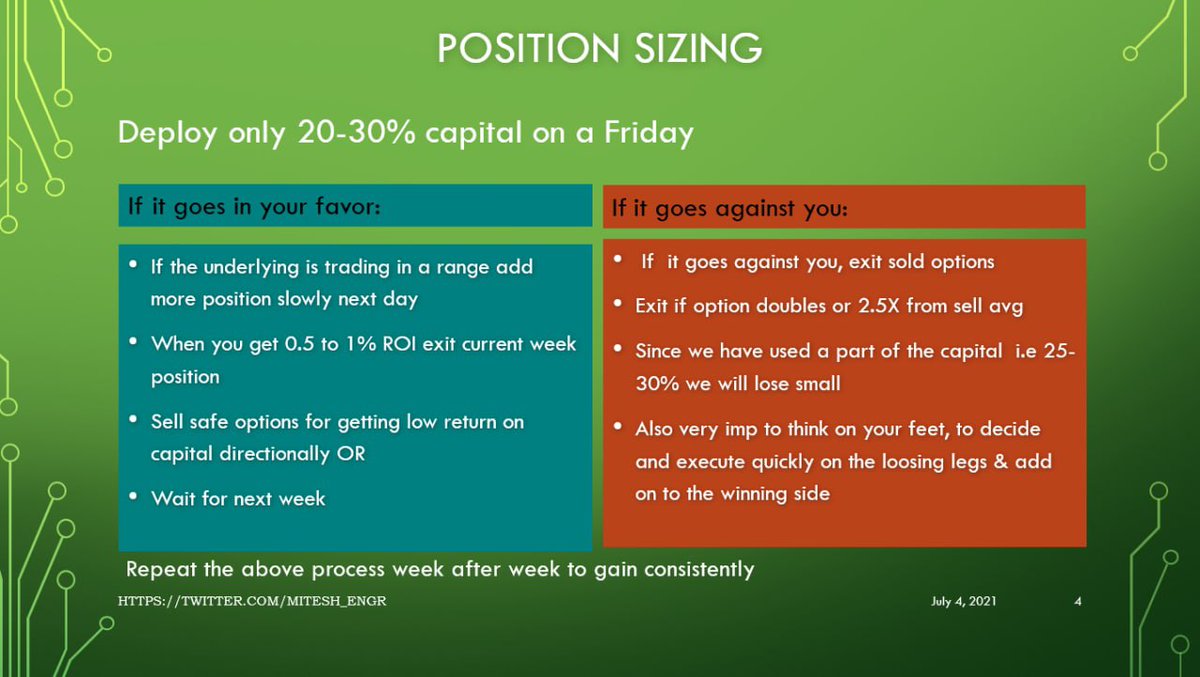
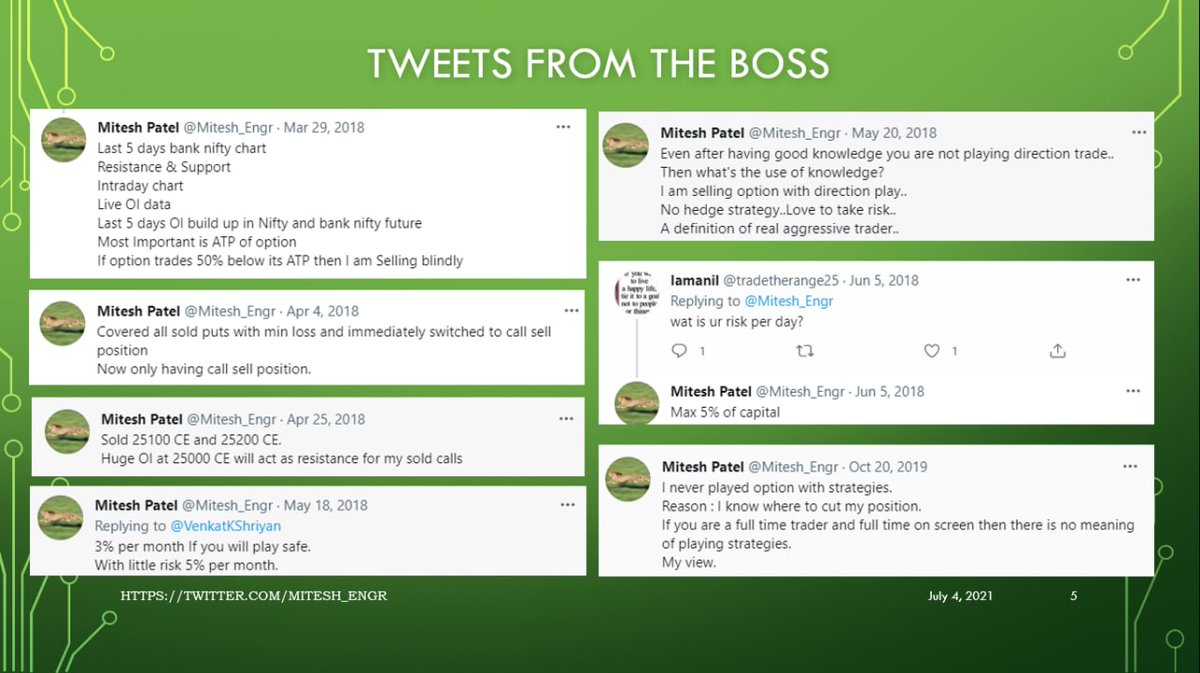
(1/15)
Loops and their multiplication groups
A thread in 15 parts
(0/15)
(1/15)
A loop is a quasigroup with an identity element. The story of why they are called loops is an interesting one and may even be true, but I will save it for another day. I am going to focus on loops in this thread.
(2/15)
- The nonzero octonions under multiplication
- The sphere S^7 under octonion multiplication
- I have discussed other examples previously:
https://t.co/q5LjmxHEIF
https://t.co/UPHSMwQo75
(3/15)
Rethinking Vector Addition
— Michael Kinyon (@ProfKinyon) December 1, 2020
or
How I Learned to Stop Worrying and Love Nonassociativity
A thread in 29 tweets
(0/28)
(4/15)
(5/15)
(6/15)
(7/15)
Now back to the general case where Q is any loop.
(8/15)
(9/15)
Loops can be studied via their multiplication and inner mapping groups. I will give one example of how this works.
(10/15)
(11/15)
1. N is the kernel of a homomorphism,
2. N is invariant under Inn(Q),
3. N is a block of Mlt(Q).
Such an N is called a normal subloop of Q. Q is simple if it has no nontrivial normal subloops.
(12/15)
Theorem (Albert 1941): A loop Q is simple if and only if Mlt(Q) is primitive.
(13/15)
More from Maths
OK, I may be guilty of a DoS attack attempt on mathematicians' brains here, so lest anyone waste too much precious brain time decoding this deliberately cryptic statement, let me do it for you. •1/15
First, as some asked, it is to be parenthesized as: “∀x.∀y.((∀z.((z∈x) ⇒ (((∀t.((t∈x) ⇒ ((t∈z) ⇒ (t∈y))))) ⇒ (z∈y)))) ⇒ (∀z.((z∈x) ⇒ (z∈y))))” (the convention is that ‘⇒’ is right-associative: “P⇒Q⇒R” means “P⇒(Q⇒R)”), but this doesn't clarify much. •2/15
Maybe we can make it a tad less abstruse by using guarded quantifiers (“∀u∈x.(…)” stands for “∀u.((u∈x)⇒(…))”): it is then “∀x.∀y.((∀z∈x.(((∀t∈x.((t∈z) ⇒ (t∈y)))) ⇒ (z∈y))) ⇒ (∀z∈x.(z∈y)))”. •3/15
Maybe a tad clearer again by writing “P(u)” for “u∈y” and leaving out the quantifier on y, viꝫ: “∀x.((∀z∈x.(((∀t∈x.((t∈z) ⇒ P(t)))) ⇒ P(z))) ⇒ (∀z∈x.P(z)))” [✯]. Now it appears as an induction principle: namely, … •4/15
… “in order to prove P(z) for all z∈x, we can assume, when proving P(z), that P(t) is already known for all t∈z∩x” (n.b.: “(∀z.(Q(z)⇒P(z)))⇒(∀z.P(z))” can be read “in order to prove P(z) for all z, we can assume Q(z) known when proving P(z)”). •5/15
\u2200x.\u2200y.((\u2200z.((z\u2208x) \u21d2 ((\u2200t.((t\u2208x) \u21d2 (t\u2208z) \u21d2 (t\u2208y)))) \u21d2 (z\u2208y))) \u21d2 (\u2200z.((z\u2208x) \u21d2 (z\u2208y))))
— Gro-Tsen (@gro_tsen) February 12, 2021
First, as some asked, it is to be parenthesized as: “∀x.∀y.((∀z.((z∈x) ⇒ (((∀t.((t∈x) ⇒ ((t∈z) ⇒ (t∈y))))) ⇒ (z∈y)))) ⇒ (∀z.((z∈x) ⇒ (z∈y))))” (the convention is that ‘⇒’ is right-associative: “P⇒Q⇒R” means “P⇒(Q⇒R)”), but this doesn't clarify much. •2/15
Maybe we can make it a tad less abstruse by using guarded quantifiers (“∀u∈x.(…)” stands for “∀u.((u∈x)⇒(…))”): it is then “∀x.∀y.((∀z∈x.(((∀t∈x.((t∈z) ⇒ (t∈y)))) ⇒ (z∈y))) ⇒ (∀z∈x.(z∈y)))”. •3/15
Maybe a tad clearer again by writing “P(u)” for “u∈y” and leaving out the quantifier on y, viꝫ: “∀x.((∀z∈x.(((∀t∈x.((t∈z) ⇒ P(t)))) ⇒ P(z))) ⇒ (∀z∈x.P(z)))” [✯]. Now it appears as an induction principle: namely, … •4/15
… “in order to prove P(z) for all z∈x, we can assume, when proving P(z), that P(t) is already known for all t∈z∩x” (n.b.: “(∀z.(Q(z)⇒P(z)))⇒(∀z.P(z))” can be read “in order to prove P(z) for all z, we can assume Q(z) known when proving P(z)”). •5/15
It is trying when mathematicians declare condescendingly that there is no point doing things because their models tell them so. Well maybe some of the assumptions don't hold up. How did that work out for the no additional risk from large events and no point in border controls...
During wave 1 cases fell very fast, faster than I think most people were expecting. Particularly in Scotland. Rt was probably ~0.5 until we started easing off.
This was despite a constant leak of cases coming out of hospitals and LTC facilities as we were rationing PPE and are policies were nowhere near ideal. There was insistence from infection control that droplet protections were sufficient. We have all learned a lot since then.
Not to mention we have learned to avoid the shit show of actively importing cases into care homes. We've learned not to repeat that. Other sectors have learned too.
We've learned a lot and there's no reason we can't control this new variant. But we will not manage if we don't try and act with clarity of purpose.
Oh for crying out loud. I don't know anyone who thinks we can get R below 0.9 with this new variant. It's 22 virus generations to even get from 50,000 cases to 5,000 at R=0.9 - that's 4 months. TTI is a complete fantasy right now: spend the money on the vaccine rollout. https://t.co/MyeBt8tC1w
— Oliver Johnson (@BristOliver) January 3, 2021
During wave 1 cases fell very fast, faster than I think most people were expecting. Particularly in Scotland. Rt was probably ~0.5 until we started easing off.
This was despite a constant leak of cases coming out of hospitals and LTC facilities as we were rationing PPE and are policies were nowhere near ideal. There was insistence from infection control that droplet protections were sufficient. We have all learned a lot since then.
Not to mention we have learned to avoid the shit show of actively importing cases into care homes. We've learned not to repeat that. Other sectors have learned too.
We've learned a lot and there's no reason we can't control this new variant. But we will not manage if we don't try and act with clarity of purpose.