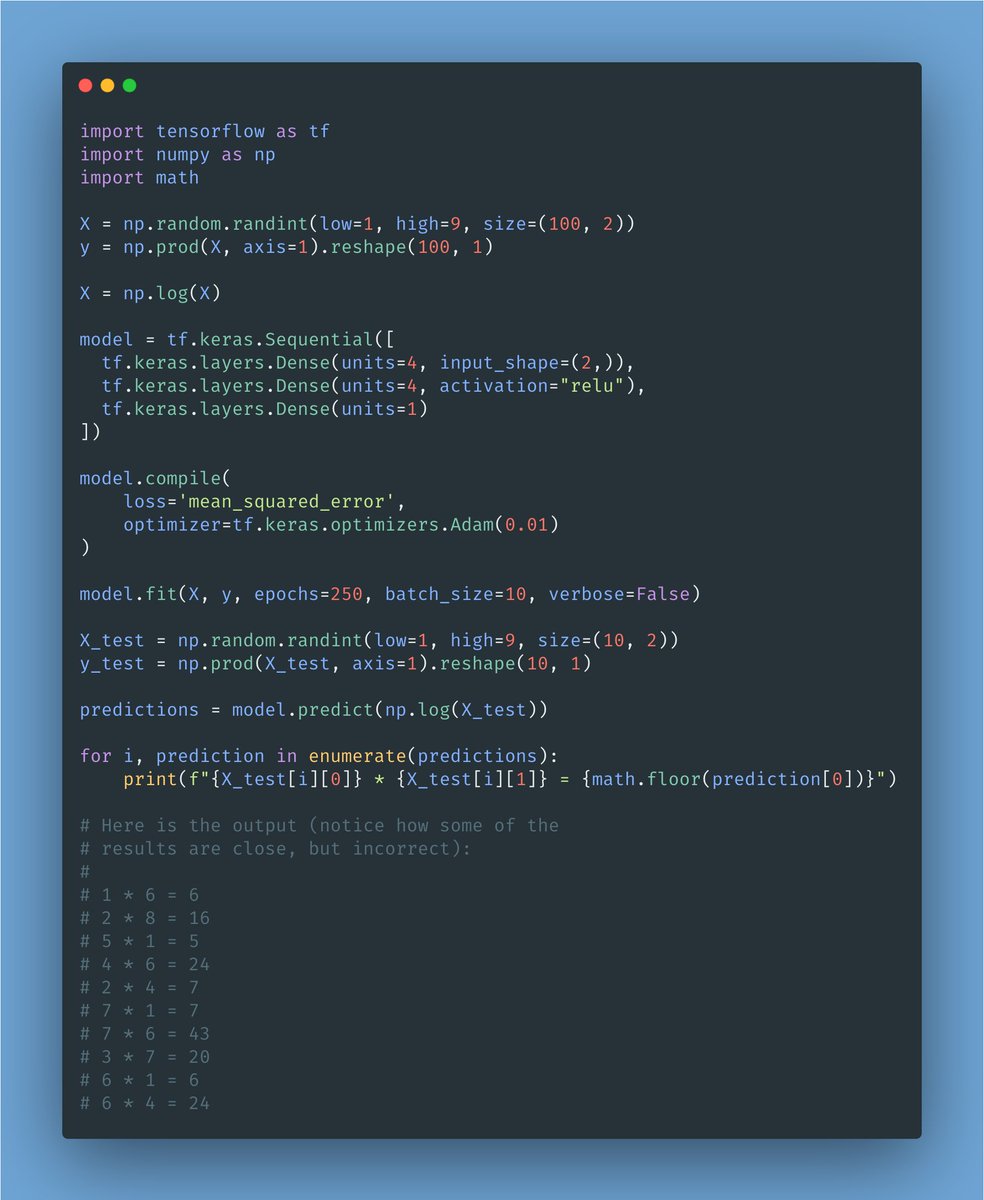
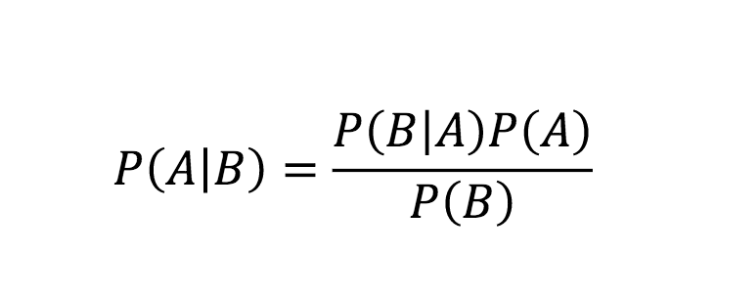I'm gonna focus here on image classification.
Let's assume you built two different models:
• Model 1: A ResNet model.
• Model 2: A one-shot model (Siamese network.)
They both solve the same problem, so you want to combine their results to pick the right answer.
The problem is that you have two models, so voting is not trivial.
What happens in this case?
• Model 1's answer: Class A
• Model 2's answer: Class B
Which one do you select?
Notice that this problem is not limited to an even number of models.
You could have 3 models, each giving you a different answer.
How do you decide which answer to choose?
There are multiple ways to approach this problem. I'll mention a few different ideas on this thread.
Important: Some of these ideas might not be feasible depending on your context. They have worked for me before on different situations, but every problem is different.
Here is a solution:
• Take 6 months' worth of data
• Compute the prior probability of every class
• Run the data through your ensemble
• Track the results of the models
• Use performance and priors to weight these results
Let's try to break these down.
The prior probability of each class tells us how likely we are to get one specific result from a model.
If I tell you that I saw a plane, you would believe me. But how about if I tell you I saw a UFO?
Planes have a higher chance of being the correct answer.
The second component is the performance of each model on every class.
For example, Model 1 might be really good at identifying planes, but Model 2 may constantly make mistakes.
This should tell us how much we should believe the results from each model.
A third component may be the score assigned by the model.
In the case of the ResNet model, the softmax probability. In the case of the one-shot model, the similarity score.
These three different features can help us evaluate each answer and decide which one is more likely to be correct.
The ensemble then becomes:
• Model 1
• Model 2
• Model 3 ← This one is the new model deciding which answer to pick.
Keep in mind that introducing a third model adds complexity to the system.
Sometimes, a simple heuristic might be a good enough solution.
It's our job to weigh the pros and cons. Better performance is just one side of the equation.
If you enjoy these threads, follow me
@svpino as I help you deconstruct machine learning and turn it into Your Next Big Thing™.
Do you have any experience dealing with ensemble voting? Any other ideas that come to mind on how to tackle this problem?