BC MATHS
Saved by @CodyyyGardner

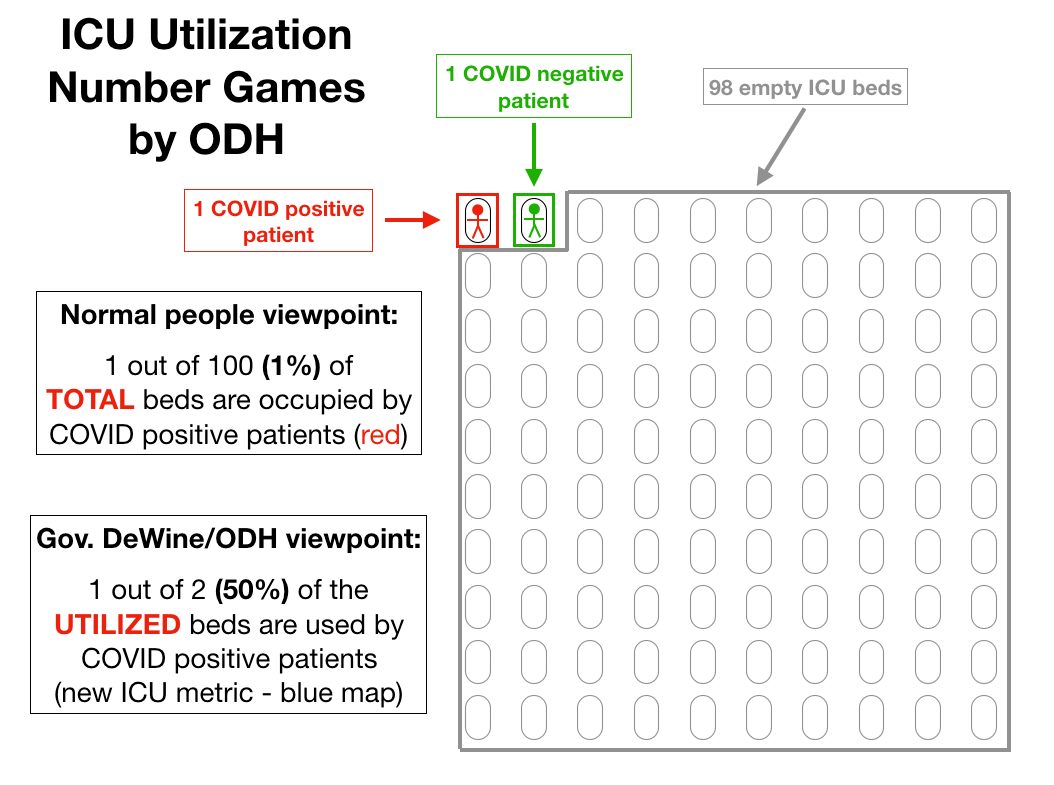
It is trying when mathematicians declare condescendingly that there is no point doing things because their models tell them so. Well maybe some of the assumptions don't hold up. How did that work out for the no additional risk from large events and no point in border controls...

 During wave 1 cases fell very fast, faster than I think most people were expecting. Particularly in Scotland. Rt was probably ~0.5 until we started easing off.
This was despite a constant leak of cases coming out of hospitals and LTC facilities as we were rationing PPE and are policies were nowhere near ideal. There was insistence from infection control that droplet protections were sufficient. We have all learned a lot since then.
Not to mention we have learned to avoid the shit show of actively importing cases into care homes. We've learned not to repeat that. Other sectors have learned too.
We've learned a lot and there's no reason we can't control this new variant. But we will not manage if we don't try and act with clarity of purpose.
We also learned from wave 1 not to abandon contact tracing and to test people as early as possible to prevent transmission chains. I.e. TTI. That still holds true. Let us not repeat the mistakes.
In fact, in March we got Rt down to that level with effectively no targeted support from TTI because we were only testing on admission (way too late). And we had so little testing capacity.
In addition, in March there was approximately zero prior immunity. Now there is a non-zero amount and that helps eat into some of the increase in transmissibility.
We have light at the end of the tunnel with vaccines and can target vaccines at those who cannot isolate (essential workers) with more scope to do this the less urgently we need to vaccinate the vulnerable. This helps psychologically and practically.
Practically, for example, having vaccinated workers in LTC and vaccinated people support the elderly is a game changer for isolation.
Rapid testing is another tool we now have that could help alongside TTI and vaccines. We have lots more at our disposal to work with.
Chasing down every case is still going to become *more* not less important. It is perfectly possible that if vaccine evading strains don't arise in the UK we will import them at some time. Will need TTI then. Goes without saying that this will also not be the last pandemic.
I suspect one reason why the TTI is constantly underestimated is that it is in practice just naturally much better at finding cases in high transmission events than no/low transmission cases. And maybe this is hard to model.
For very many human reasons that are just intuitively apparent to anyone who has trained in taking a history from a patient: you have a shared agenda to get to the most important information about the most important events. And you build a shared understanding of what those are.
Perhaps the cases missed are much much more likely to be in the 80% or so of people who don't infect someone else.
For all the obsession with overdispersion of SARS2 and HIT, I actually think this is where it makes the most difference. I think its why many mathematicians seem baffled or underenthused by the East Asian response... sure it works in practice, but it makes no sense in theory.
In addition, just because something doesn't solve the problem on it's own doesn't mean it doesn't help solve the problem.
I don't mean to single out @BristOliver for this rant, so sorry for that. I find your takes on the whole very interesting so hope you don't block me. This just really bugged me on the back of a recent chat with a friend who is a public health trainee.
She has been working very hard on TTI all year and feels drained, and, I think, underappreciated. And I feel strongly that we have not championed this essential work enough. So much so that, I'm told, it is now increasingly common that when contacting people they get vile abuse.
A bit less of this: "there's no point in doing that thing that has been the backbone of every competent outbreak response for over 150 years and that WHO insists is key and that all Covid-controlling countries have invested in" would be nice. (Paraphrasing no-one in particular.)
Even if only out of respect for all the people working their asses off to get it done in incredibly difficult circumstances.

More from Maths

Gro-Tsen
Gro-Tsen
@gro_tsen
OK, I may be guilty of a DoS attack attempt on mathematicians' brains here, so lest anyone waste too much precious brain time decoding this deliberately cryptic statement, let me do it for you. •1/15


First, as some asked, it is to be parenthesized as: “∀x.∀y.((∀z.((z∈x) ⇒ (((∀t.((t∈x) ⇒ ((t∈z) ⇒ (t∈y))))) ⇒ (z∈y)))) ⇒ (∀z.((z∈x) ⇒ (z∈y))))” (the convention is that ‘⇒’ is right-associative: “P⇒Q⇒R” means “P⇒(Q⇒R)”), but this doesn't clarify much. •2/15

Maybe we can make it a tad less abstruse by using guarded quantifiers (“∀u∈x.(…)” stands for “∀u.((u∈x)⇒(…))”): it is then “∀x.∀y.((∀z∈x.(((∀t∈x.((t∈z) ⇒ (t∈y)))) ⇒ (z∈y))) ⇒ (∀z∈x.(z∈y)))”. •3/15

Maybe a tad clearer again by writing “P(u)” for “u∈y” and leaving out the quantifier on y, viꝫ: “∀x.((∀z∈x.(((∀t∈x.((t∈z) ⇒ P(t)))) ⇒ P(z))) ⇒ (∀z∈x.P(z)))” [✯]. Now it appears as an induction principle: namely, … •4/15

… “in order to prove P(z) for all z∈x, we can assume, when proving P(z), that P(t) is already known for all t∈z∩x” (n.b.: “(∀z.(Q(z)⇒P(z)))⇒(∀z.P(z))” can be read “in order to prove P(z) for all z, we can assume Q(z) known when proving P(z)”). •5/15
MATHS
Spencer Greenberg \U0001f50d
Spencer Greenberg 🔍...
@SpencrGreenberg
Ten components of being compassionate to yourself:

1. Self-friendship: treat yourself at least as well as you would treat a friend who is going through the same situation

[thread]

2. Worthiness: remember that you have value (as all people do), and that your happiness and preferences matter.

3. Self-talk: notice when you are saying something mean to yourself (aloud, or in your head), and rephrase it in a gentler, kinder, more considerate way.

4. Connectedness: reflect on the fact that, whatever challenge you are facing, there are others who are also facing a similar challenge. You are not alone in your pain.

5. Change: note that everything changes with time. If you are dealing with feelings that are difficult to stand at this moment, they will subside. This too shall pass. Things are usually not as important or permanent as they seem to us in the moment that we are focused on them.

6. Self-empathy: orient towards yourself with tenderness, understanding and compassion, especially when you are suffering. Take on the perspective that you would towards a child or loved one that was hurting.
LIFE , MATHS
Advertisement
Understanding Ohio COVID Data
Understanding Ohio COV...
@ohio_data
⬇️⬇️⬇️ The "Math" of Fear

As it is Thursday, I have a post for you today in anticipation of Gov. DeWine's new Maps of Fear which he has tried to phase in. I have previously discussed both the new red and blue maps and their issues -

- but today I hope to illustrate even more clearly what level of manipulation is going on, particularly with the new blue 'ICU Utilization' map.

Attached I have two images.

The first is a hyper-simplistic (and unrealistic) but illustrative example of the calculations that the new blue map goes through to arrive at its numbers.


Instead of telling us the percent of beds occupied by COVID+ (not necessarily ill *with* COVID, but testing positive) - the governor and ODH only calculates the percentage of COVID+ out of just the *used* beds.

In the first image, I have an example of a 100 bed ICU with just two patients - one COVID positive (red) and one COVID negative (green). The other 98 beds are empty and able to accept new patients.
MATHS
Algebra Etc.
Algebra Etc.
@AlgebraFact
How to mentally compute the cube root of the cube of a two digit number.

Thread (1/10)

In base 10, the last digits of the cubes of digits are distinct.

If d = 0, 1, 4, 5, 6, or 9, then d^3 ends in d.

If d = 2, 3, 7, or 8, then d^3 ends in 10-d.

(2/10)

So if you're given the cube of an integer, you can figure out the last digit of the cube root.

For example, if 50653 is the cube of an integer, it's the cube of a number ending in 7.

(3/10)

Let n = 10a + b be a two-digit number, with a and b single digit numbers.

Then 10a <= n <= 10(a+1), and so n^3 is between (10a)^3 and (10(a+1))^3, i.e. between 1000 a^3 and 1000 (a+1)^3.

(4/10)

So suppose x is the cube of a two-digit number n = 10a + b.

Chop off the last three digits of x.

Then a, the first digit of n, is the largest number whose cube is no greater than what's left of x.

(5/10)
MATHS
Handwaving Freakoutery
Handwaving Freakoutery
@Freakoutery
The main problem with "Lift All Voices" as a justification for the Black National Anthem is the word "All." In order to achieve "All," the Woke are going to have to cook up more different unique national anthems than they have gender pronouns.

Mathematically speaking.

1/

And why would the Black community be the first to get their own anthem over the American Indians? The Indians used to have all the land, and they still do have some of it.

(use of "American Indian" here is intentional, as that's what they prefer to call themselves)

2/

This "inclusion by division" game is just the "separate but equal" logic for 1950s segregation reskinned, but when the Woke self segregate, they self segregate based on Krenshaw's Intersectional Matrix of Oppression, which in Theory is necessarily near infinite in size.

3/

When the Woke did this with gender pronouns we went from 2 genders to 37 genders to infinite genders in the span of about 5 years, but the trans folks discovered this really didn't help them out on Tinder, so they pivoted back to "trans women are women" to try and get dates.

4/

The only people left doing the "gender pronouns" game are the ones signaling their Wokeness on Twitter to their in-group, the trans women in the dating community aren't even doing it anymore. They've gone back to 2.

5/
MATHS

You May Also Like

Mitesh Patel
Mitesh Patel
@Mitesh_Engr
How to sell option?
Here let me explain through simple math.
Say BN at 30000
30000 straddle trading at combine premium 800 ( based on current volatility)
Put at 400
Call at 400
You don’t know direction. Sold both.

If move will not come than both will decrease gradually.

At day end it will come down to 720-740 if move will not come. Difference is your profit.

Now case 2:
Move started.
At one points combine premium will start increasing.
Say 810.
Exit immediately. No need to do adjustment.
Let market settle.

Sell again straddle once market settle.
Now repeat same thing.

Straddle selling webinar over.
Good luck.

One can keep SL 550 for both strike to escape from sudden movement.
OPTIONSLEARNING , MITESHOPTIONS
Jaya_Upadhyaya
Jaya_Upadhyaya
@Jayalko1
BANASHANKARI AMMA, NEAR BADAMI (KAR)
#bharatmandir #navratri2021

Originally built by Chalukyas in 7th century. Devi Banashankari was their family deity. This image of Banashankari Amma was installed by Jagadekamalla I in 630 AD.

Later renovations were done by Marathas.


Once, a demon Durgamasur was troubling the people of this area. Answering the prayers of Devas, Ma Parvati emerged from the yajna fire as Banashankari and killed Durgamasur.
This area has rich forests of coconut, betel nut and other trees.
@GunduHuDuGa


It is said that during a severe famine, Devi provided vegetables and fruits to the people of this area.
Hence, she is also worshipped here as Shakambhari.
In the annual festival called Banashankari jatre, a Rath yatra takes place and Devi moves around the city in the chariot.
ALL
Advertisement
Sam
Sam
@SamKhan999
This day was inevitable. Indian Muslims always lived in La La Land. They bad mouthed real well wishers & slept with the enemy who never considered them as part of them. In Gulf, Indian Muslims were busy with Javed Akhtar & Sonu Nigam. Never interacted with South Asian diaspora

Now when Indian Muslims are thrown to wolves it’s Pakistani & Bangladeshi Muslims with whom they kept distance are the only ones feeling their pain. None of the people who they invited for Eid Milan. Qawali & Mushaira are there for them. Such people invoke wrath upon themselves

Indian Muslims never spoke for Kashmiri Muslims. Distancing from separatist was understandable but we never even bothered to highlight their human rights violation & rapes carried out by forces. We could have sent them humanitarian help we didn’t. Our silence made us complicit.

When Sania Mirza married Shoaib Malik it was something legal. A Muslim married another Muslim. Entire Hindutva media went after her. They launched a witch-hunt for months. No Indian Muslim stood by her. All were silent. Now days come when Muslims are arrested for marrying a Hindu

Indian Muslims particularly the elite downplayed communalism in India by saying it will pass or Hindu majority is good. Fringe are bad. They misguiding others. Muslims were always others. Indians were happy to see Muslims sing & dance & eat their food but never considered as own
INDIA
ArmaniTalks \U0001f399\U0001f525
ArmaniTalks 🎙🔥...
@ArmaniTalks
Your Most PRECIOUS Currencies:

-Energy

-Time

-Attention

-Trust

-Love

-Loyalty

-Respect

Only give these currencies to high value people. Never spend these currencies on low value shitheads eg: trolls, weasels, snakes, naysayers etc.

'Wait, I thought money was the most important currency?'

Nah.

Once you adopt abundance mentality, you realize their is no shortage of money.

Making the dollars your most important currency will have you leading an empty life.

Time to flip your perspective.

👇

▪Energy

When you strip yourself to the core, you are an emotional creature.

Emotions are your internal worlds energy.

Harnessing that energy is crucial for leveraging yourself to obtain whatever you want.

You have a finite amount everyday, so spend it wisely.

▪Time

A second that is lost will never be returned.

You start valuing the hell out of this currency the more you mature.

As the years start adding up, you realize time is precious.

You must always have a scarcity mindset towards time.

Once you do so, you will not be lazy.

▪Attention

You can be here, but not present.

Attention is completely mental.

Giving someone your attention means you are clearing up mental bandwidth to make room for them.

Only give your attention to people who help you grow.

For the negative ones?

Ignore their existence
LIFE
EverythingOppresses
EverythingOppresses
@SoOppressed
The first area to focus on is diversity. This has become a dogma in the tech world, and despite the fact that tech is one of the most meritocratic industries in the world, there are constant efforts to promote diversity at the expense of fairness, merit and competency. Examples:

USC's Interactive Media & Games Division cancels all-star panel that included top-tier game developers who were invited to share their experiences with students. Why? Because there were no women on the

ElectronConf is a conf which chooses presenters based on blind auditions; the identity, gender, and race of the speaker is not known to the selection team. The results of that merit-based approach was an all-male panel. So they cancelled the conference.

Apple's head of diversity (a black woman) got in trouble for promoting a vision of diversity that is at odds with contemporary progressive dogma. (She left the company shortly after this

Also in the name of diversity, there is unabashed discrimination against men (especially white men) in tech, in both hiring policies and in other arenas. One such example is this, a developer workshop that specifically excluded men: https://t.co/N0SkH4hR35
TECH