It's 2021! Time for a crash course in four terms that I often see mixed up when people talk about testing: sensitivity, specificity, positive predictive value, negative predictive value.
These terms help us talk about how accurate a test is, but from different viewpoints. 1/
A test that is very *specific* will be very good at accurately ruling out infection in people who are not infected. 3/
Of the 10 people infected, 8 test + (true +), 2 test - (false -).
Of the 90 people uninfected, 89 test - (true -), 1 tests + (false +). 7/
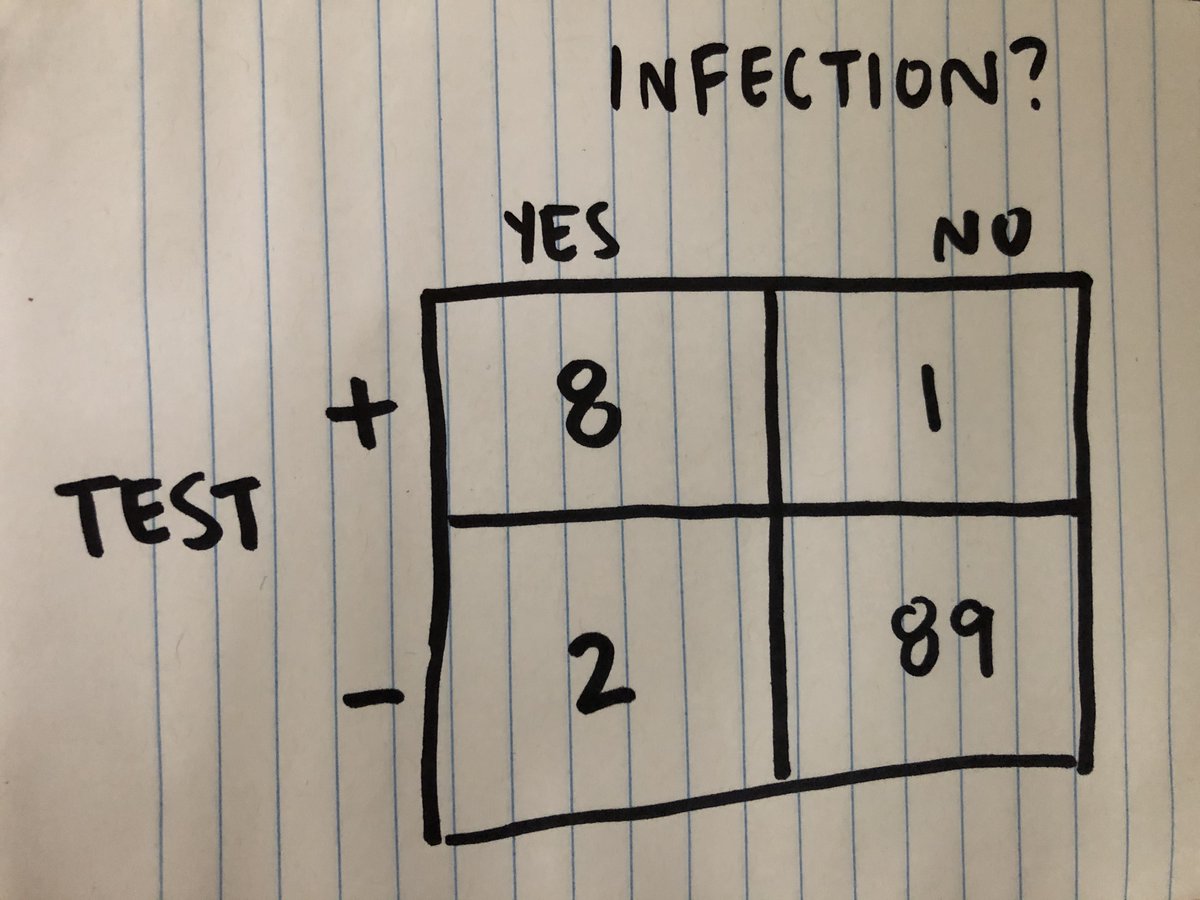
The test's positive predictive value is true positives/(true positives + false positives): 8/9, or 88.9%. It's the proportion of positives, out of all the positives, that were accurate. 10/
More from Education
OK I am going to be tackling this as surveillance/open source intel gathering exercise, because that is my background. I blew away 3 years of my life doing site acquisition/reconnaissance for a certain industry that shall remain unnamed and believe there is significant carryover.
This is NOT going to be zillow "here is how to google school districts and find walmart" we are not concerned with this malarkey, we are homeschooling and planting victory gardens and having gigantic happy families.
With that said, for my frog and frog-adjacent bros and sisters:
CHOICE SITES:
Zillow is obvious one, but there are many good sites like Billy Land, Classic Country Land, Landwatch, etc. and many of these specialize in owner financing (more on that later.) Do NOT treat these as authoritative sources - trust plat maps and parcel viewers.
TARGET IDENTIFICATION AND EVALUATION:
Okay, everyone knows how to google "raw land in x state" but there are other resources out there, including state Departments of Natural Resources, foreclosure auctions, etc. Finding the land you like is the easy part. Let's do a case study.
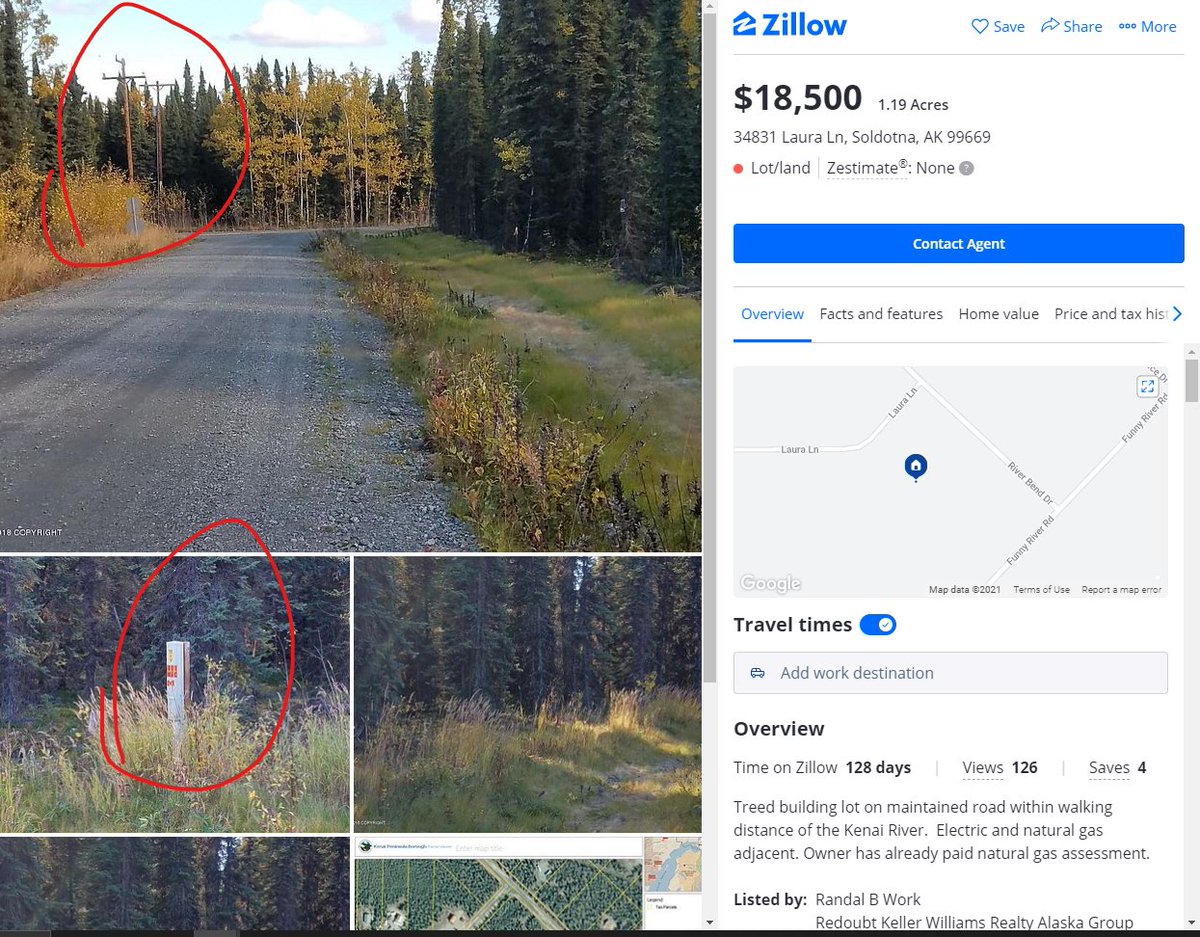
I'm going to target using an "off-grid but not" algorithm. This is a good piece in my book - middle of nowhere but still trekkable to civilization.
Note: visible power, power/fiber pedestal, utility corridor, nearby commercial enterprise(s), and utility pole shadows visible.
If I did thred on finding/acquiring decent raw land would that be something pepo are interested in
— Ovcharka (@ouroboros_outis) January 18, 2021
I think I know a bunch of weird tips/tricks for selection at this point that it might help u guys, lemme know
This is NOT going to be zillow "here is how to google school districts and find walmart" we are not concerned with this malarkey, we are homeschooling and planting victory gardens and having gigantic happy families.
With that said, for my frog and frog-adjacent bros and sisters:
CHOICE SITES:
Zillow is obvious one, but there are many good sites like Billy Land, Classic Country Land, Landwatch, etc. and many of these specialize in owner financing (more on that later.) Do NOT treat these as authoritative sources - trust plat maps and parcel viewers.
TARGET IDENTIFICATION AND EVALUATION:
Okay, everyone knows how to google "raw land in x state" but there are other resources out there, including state Departments of Natural Resources, foreclosure auctions, etc. Finding the land you like is the easy part. Let's do a case study.
I'm going to target using an "off-grid but not" algorithm. This is a good piece in my book - middle of nowhere but still trekkable to civilization.
Note: visible power, power/fiber pedestal, utility corridor, nearby commercial enterprise(s), and utility pole shadows visible.

You May Also Like
I hate when I learn something new (to me) & stunning about the Jeff Epstein network (h/t MoodyKnowsNada.)
Where to begin?
So our new Secretary of State Anthony Blinken's stepfather, Samuel Pisar, was "longtime lawyer and confidant of...Robert Maxwell," Ghislaine Maxwell's Dad.

"Pisar was one of the last people to speak to Maxwell, by phone, probably an hour before the chairman of Mirror Group Newspapers fell off his luxury yacht the Lady Ghislaine on 5 November, 1991." https://t.co/DAEgchNyTP

OK, so that's just a coincidence. Moving on, Anthony Blinken "attended the prestigious Dalton School in New York City"...wait, what? https://t.co/DnE6AvHmJg
Dalton School...Dalton School...rings a
Oh that's right.
The dad of the U.S. Attorney General under both George W. Bush & Donald Trump, William Barr, was headmaster of the Dalton School.
Donald Barr was also quite a
I'm not going to even mention that Blinken's stepdad Sam Pisar's name was in Epstein's "black book."
Lots of names in that book. I mean, for example, Cuomo, Trump, Clinton, Prince Andrew, Bill Cosby, Woody Allen - all in that book, and their reputations are spotless.

Where to begin?
So our new Secretary of State Anthony Blinken's stepfather, Samuel Pisar, was "longtime lawyer and confidant of...Robert Maxwell," Ghislaine Maxwell's Dad.

"Pisar was one of the last people to speak to Maxwell, by phone, probably an hour before the chairman of Mirror Group Newspapers fell off his luxury yacht the Lady Ghislaine on 5 November, 1991." https://t.co/DAEgchNyTP

OK, so that's just a coincidence. Moving on, Anthony Blinken "attended the prestigious Dalton School in New York City"...wait, what? https://t.co/DnE6AvHmJg
Dalton School...Dalton School...rings a
Oh that's right.
The dad of the U.S. Attorney General under both George W. Bush & Donald Trump, William Barr, was headmaster of the Dalton School.
Donald Barr was also quite a
Donald Barr had a way with words. pic.twitter.com/JdRBwXPhJn
— Rudy Havenstein, listening to Nas all day. (@RudyHavenstein) September 17, 2020
I'm not going to even mention that Blinken's stepdad Sam Pisar's name was in Epstein's "black book."
Lots of names in that book. I mean, for example, Cuomo, Trump, Clinton, Prince Andrew, Bill Cosby, Woody Allen - all in that book, and their reputations are spotless.
























