2/
One might say that physicists study the symmetry of nature, while mathematicians study the nature of symmetry.
1/
2/
3/
1) Closure: a⊡b is in G.
2) Associativity: (a⊡b)⊡c = a⊡(b⊡c)
3) Identity: e⊡a = a⊡e = a.
4) Inverse: There exists an element a* such that a*⊡a = a⊡a* = e.
4/
5/
then μ: G ⟼ H is a "group morphism" if for all elements of G:
μ(a⊡b) = μ(a)⊠μ(b). Note that for all a:
μ(a)⊠ε = μ(a) = μ(a⊡e) = μ(a)⊠μ(e)
and hence μ(e)=ε; Similarly it can be shown that
μ(a*) = μ(a)*.
- the *Baby Monster*, *B*, of size
2⁴¹ ⋅ 3¹³ ⋅ 5⁶ ⋅ 7² ⋅ 11 ⋅ 13 ⋅ 17 ⋅ 19 ⋅ 23 ⋅ 31 ⋅ 47; and
2⁴⁶ ⋅ 3²⁰ ⋅ 5⁹ ⋅ 7⁶ ⋅ 11² ⋅ 13³ ⋅ 17 ⋅ 19 ⋅ 23 ⋅ 29 ⋅ 31 ⋅ 41 ⋅ 47 ⋅ 59 ⋅ 71.
Counting up the number of distinct primes in that last number gives us 15.
The number of distinct prime factors
in the size, n, of the *Monster Group* M
is
15.
More from Maths
Loops and their multiplication groups
A thread in 15 parts
(0/15)
Recall that a quasigroup (Q,*) is a set Q with a binary operation * such that for each a,b in Q, the equations a*x=b and y*a=b have unique solutions x,y. Groups are quasigroups and this property is usually one of the first things proved in elementary group theory.
(1/15)
Note that we don't assume associativity of *!
A loop is a quasigroup with an identity element. The story of why they are called loops is an interesting one and may even be true, but I will save it for another day. I am going to focus on loops in this thread.
(2/15)
Natural examples of nonassociative loops:
- The nonzero octonions under multiplication
- The sphere S^7 under octonion multiplication
- I have discussed other examples
For each x in a loop Q, define the left & right translations L_x, R_x : Q->Q by L_x(y)=xy and R_x(y)=yx. These mappings are permutations of Q. The composition L_x L_y of two left translations is not necessarily a left translation because Q is not necessarily associative.
(4/15)
A thread in 15 parts
(0/15)
Recall that a quasigroup (Q,*) is a set Q with a binary operation * such that for each a,b in Q, the equations a*x=b and y*a=b have unique solutions x,y. Groups are quasigroups and this property is usually one of the first things proved in elementary group theory.
(1/15)
Note that we don't assume associativity of *!
A loop is a quasigroup with an identity element. The story of why they are called loops is an interesting one and may even be true, but I will save it for another day. I am going to focus on loops in this thread.
(2/15)
Natural examples of nonassociative loops:
- The nonzero octonions under multiplication
- The sphere S^7 under octonion multiplication
- I have discussed other examples
Rethinking Vector Addition
— Michael Kinyon (@ProfKinyon) December 1, 2020
or
How I Learned to Stop Worrying and Love Nonassociativity
A thread in 29 tweets
(0/28)
For each x in a loop Q, define the left & right translations L_x, R_x : Q->Q by L_x(y)=xy and R_x(y)=yx. These mappings are permutations of Q. The composition L_x L_y of two left translations is not necessarily a left translation because Q is not necessarily associative.
(4/15)
OK, I may be guilty of a DoS attack attempt on mathematicians' brains here, so lest anyone waste too much precious brain time decoding this deliberately cryptic statement, let me do it for you. •1/15
First, as some asked, it is to be parenthesized as: “∀x.∀y.((∀z.((z∈x) ⇒ (((∀t.((t∈x) ⇒ ((t∈z) ⇒ (t∈y))))) ⇒ (z∈y)))) ⇒ (∀z.((z∈x) ⇒ (z∈y))))” (the convention is that ‘⇒’ is right-associative: “P⇒Q⇒R” means “P⇒(Q⇒R)”), but this doesn't clarify much. •2/15
Maybe we can make it a tad less abstruse by using guarded quantifiers (“∀u∈x.(…)” stands for “∀u.((u∈x)⇒(…))”): it is then “∀x.∀y.((∀z∈x.(((∀t∈x.((t∈z) ⇒ (t∈y)))) ⇒ (z∈y))) ⇒ (∀z∈x.(z∈y)))”. •3/15
Maybe a tad clearer again by writing “P(u)” for “u∈y” and leaving out the quantifier on y, viꝫ: “∀x.((∀z∈x.(((∀t∈x.((t∈z) ⇒ P(t)))) ⇒ P(z))) ⇒ (∀z∈x.P(z)))” [✯]. Now it appears as an induction principle: namely, … •4/15
… “in order to prove P(z) for all z∈x, we can assume, when proving P(z), that P(t) is already known for all t∈z∩x” (n.b.: “(∀z.(Q(z)⇒P(z)))⇒(∀z.P(z))” can be read “in order to prove P(z) for all z, we can assume Q(z) known when proving P(z)”). •5/15
\u2200x.\u2200y.((\u2200z.((z\u2208x) \u21d2 ((\u2200t.((t\u2208x) \u21d2 (t\u2208z) \u21d2 (t\u2208y)))) \u21d2 (z\u2208y))) \u21d2 (\u2200z.((z\u2208x) \u21d2 (z\u2208y))))
— Gro-Tsen (@gro_tsen) February 12, 2021
First, as some asked, it is to be parenthesized as: “∀x.∀y.((∀z.((z∈x) ⇒ (((∀t.((t∈x) ⇒ ((t∈z) ⇒ (t∈y))))) ⇒ (z∈y)))) ⇒ (∀z.((z∈x) ⇒ (z∈y))))” (the convention is that ‘⇒’ is right-associative: “P⇒Q⇒R” means “P⇒(Q⇒R)”), but this doesn't clarify much. •2/15
Maybe we can make it a tad less abstruse by using guarded quantifiers (“∀u∈x.(…)” stands for “∀u.((u∈x)⇒(…))”): it is then “∀x.∀y.((∀z∈x.(((∀t∈x.((t∈z) ⇒ (t∈y)))) ⇒ (z∈y))) ⇒ (∀z∈x.(z∈y)))”. •3/15
Maybe a tad clearer again by writing “P(u)” for “u∈y” and leaving out the quantifier on y, viꝫ: “∀x.((∀z∈x.(((∀t∈x.((t∈z) ⇒ P(t)))) ⇒ P(z))) ⇒ (∀z∈x.P(z)))” [✯]. Now it appears as an induction principle: namely, … •4/15
… “in order to prove P(z) for all z∈x, we can assume, when proving P(z), that P(t) is already known for all t∈z∩x” (n.b.: “(∀z.(Q(z)⇒P(z)))⇒(∀z.P(z))” can be read “in order to prove P(z) for all z, we can assume Q(z) known when proving P(z)”). •5/15
You May Also Like
Keep dwelling on this:
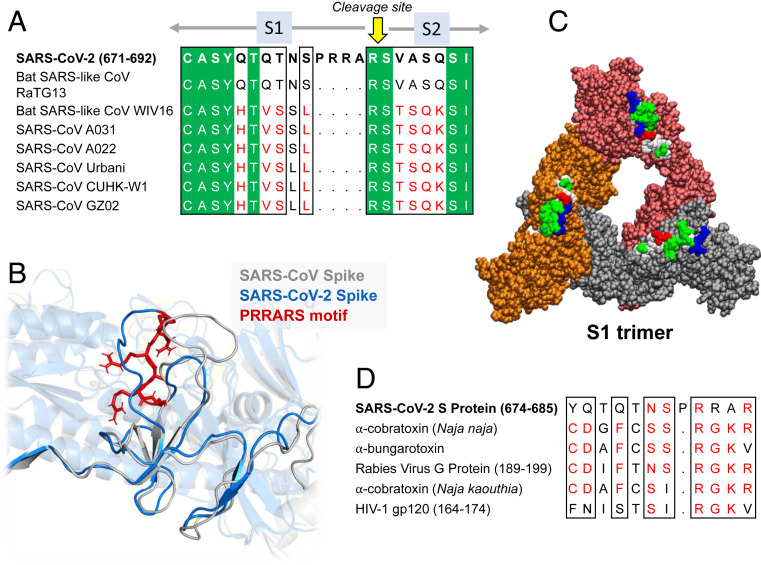
Further Examination of the Motif near PRRA Reveals Close Structural Similarity to the SEB Superantigen as well as Sequence Similarities to Neurotoxins and a Viral SAg.
The insertion PRRA together with 7 sequentially preceding residues & succeeding R685 (conserved in β-CoVs) form a motif, Y674QTQTNSPRRAR685, homologous to those of neurotoxins from Ophiophagus (cobra) and Bungarus genera, as well as neurotoxin-like regions from three RABV strains
(20) (Fig. 2D). We further noticed that the same segment bears close similarity to the HIV-1 glycoprotein gp120 SAg motif F164 to V174.
https://t.co/EwwJOSa8RK
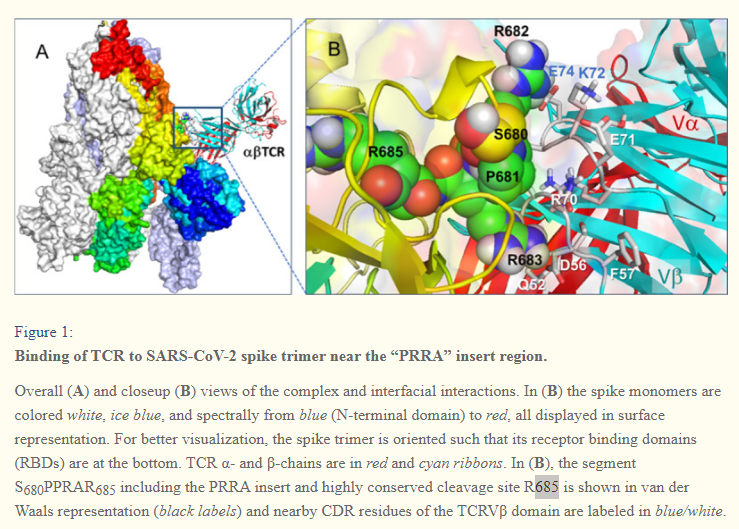
In (B), the segment S680PPRAR685 including the PRRA insert and highly conserved cleavage site *R685* is shown in van der Waals representation (black labels) and nearby CDR residues of the TCRVβ domain are labeled in blue/white
https://t.co/BsY8BAIzDa
Sequence Identity %
https://t.co/BsY8BAIzDa
Y674 - QTQTNSPRRA - R685
Similar to neurotoxins from Ophiophagus (cobra) & Bungarus genera & neurotoxin-like regions from three RABV strains
T678 - NSPRRA- R685
Superantigenic core, consistently aligned against bacterial or viral SAgs

Further Examination of the Motif near PRRA Reveals Close Structural Similarity to the SEB Superantigen as well as Sequence Similarities to Neurotoxins and a Viral SAg.
The insertion PRRA together with 7 sequentially preceding residues & succeeding R685 (conserved in β-CoVs) form a motif, Y674QTQTNSPRRAR685, homologous to those of neurotoxins from Ophiophagus (cobra) and Bungarus genera, as well as neurotoxin-like regions from three RABV strains
(20) (Fig. 2D). We further noticed that the same segment bears close similarity to the HIV-1 glycoprotein gp120 SAg motif F164 to V174.
https://t.co/EwwJOSa8RK

In (B), the segment S680PPRAR685 including the PRRA insert and highly conserved cleavage site *R685* is shown in van der Waals representation (black labels) and nearby CDR residues of the TCRVβ domain are labeled in blue/white
https://t.co/BsY8BAIzDa

Sequence Identity %
https://t.co/BsY8BAIzDa
Y674 - QTQTNSPRRA - R685
Similar to neurotoxins from Ophiophagus (cobra) & Bungarus genera & neurotoxin-like regions from three RABV strains
T678 - NSPRRA- R685
Superantigenic core, consistently aligned against bacterial or viral SAgs