BC MATHS
Saved by @Alex1Powell

In light of my tweet thread about the category of finite sets and commutative monoids (https://t.co/jnY0wZZbxq), I thought I might try to say what the analogue is for braided monoidal things (although much of this is still somewhat hypothetical).

 It's also just kind of a cool combinatorial structure! I've been talking to @CreeepyJoe about this lately, as well as @grassmannian.
The first thing you have to know is that, in a braided monoidal category you can still have commutative monoids. Since a braided monoidal category C has a "twist" map for every object β(x):x⊗x→x⊗x, if x is a monoid you can ask for the following diagram to commute:
Remember that being symmetric monoidal just means that if you take the twist map above and do it twice, you get the identity map, but braided monoidal doesn't mean that. But it's okay! You can still define commutative monoids here.
But so anyway, we can talk about commutative monoids in braided monoidal categories.
So we can talk about "the free braided monoidal category containing a commutative monoid," which I'll denote V. One way to say precisely what that means is that for any other braided monoidal category C, the category of braided monoidal functors BrFun(V,C) is equivalent to the…
…category of commutative monoids in C. This should be compared to the fact that symmetric monoidal functors from FinSet (with coproduct as "tensor product") into a symmetric monoidal category are equivalent to commutative monoids in that category.
So we want the same thing for braided monoidal categories. It turns out that this is NOT just FinSet again. A simple reason why is to think about what a braided monoidal category need.
One thing it needs is the following: given any object x in a braided monoidal category, there should be actions of the braid group on n strands, B_n, on the n-fold tensor product xⁿ.
Now, FinSet has this property since there are maps B_n→S_n that take a braid's "underlying permutation," but think about what it means to be "freely generated."
Recall, for instance that the free group on 2 generators {a,b} just takes all possible words on a and b, e.g. ab, abb, ababababaaaa, aaaba, etc. So if we want to freely generate a braided monoidal category then we need to freely install all these braid group actions.
I.e. for each n-fold tensor product xⁿ we should just kind of freely produce a new object βxⁿ for each β∈B_n (and then mod out by the relevant relations so, like, σ(β(xⁿ))=σβxⁿ, or whatever. And this isn't what happens in FinSet.
In FinSet there are lots of braids that act the same way on n-fold tensor products, since we've only remembered the underlying permutation of the braid. So then what IS the free braided monoidal category containing a commutative monoid?
It's interesting to me because the answer to this question doesn't seem to be nearly as well known as the answer to the question "What is the free symmetric monoidal category containing a commutative monoid?" (i.e. FinSet).
The answer is the category of so-called "vines," which is why I'm calling it V. Honestly I feel a bit weird about saying the word "vines" so much. It feels a bit "cranky," like I'm going to go to my grave screaming about this bizarre structure I'm heavily invested in. Anyway...
Let's talk about what this category looks like. First of all, its objects are the natural numbers (which obviously include zero). The morphisms are a bit trickier, and probably easiest to describe somewhat geometrically.
Given two natural numbers n and m, to describe a morphism n→m I want to start by fixing n points on the line (x,0,1) in ℝ³ and m points on the line (x,0,0).
For convenience you can imagine them stacked right above one another, so for 2→3 you can take {(1,0,1), (2,0,1)} and {(1,0,0),(2,0,0),(3,0,0)}, if you like, although ultimately it won't matter.
Then a morphism from n to m is a collection of n piecewise-linear arcs starting at the top points and moving at unit speed to the bottom points satisfying the condition that IF two arcs collide at time t then they are identical until they get to a bottom point.
The picture of a "vine" is something like this (where I've "smoothed" the piecewise-linearity because it's not really important):
It's also important that I do something akin to taking "isotopy classes" of vines. I don't want to differentiate between two vines if one is just the other wiggled around, so long as the strands don't violate the rules. Something like this:
A couple things to notice: I can move the time that two strands collide up and down however I want. Also notice that a bottom point need not have anything "incoming." We'll see a consequence of that when we get to thinking about composition.

T.G.
Lavers studied the set of such things in the case that n=m and showed that it had a monoid structure in this paper: https://t.co/DvhCj4449T

He also showed that every vine decomposes as a braid followed by a planar tree.
This is pretty non-trivial, but if you get out some shoelaces and mess around you can probably convince yourself it's true. I think of the process of "isotoping" a vine into this form as "combing" it, in the same way that you "comb" a braid.
Here's another funky consequence of these axioms. These two vines are identified:
More generally, a vine has a sort of "canonical" form where it's a braid stacked on top of a planar tree such that if we only look at the strands that hit a chosen bottom point then the braid on those strands is the trivial braid.
If you go back to that picture up there it's a little tricky to see, but starting at the bottom you can kind of push the strands around (since they're allowed to approach that bottom point from any angle in ℝ³) and slowly unwind the braid. That's going to be important later.
Now how do we compose a vine n→m with a vine m→k? The short answer is that we "stack them" like we stack braids in the braid group. You can probably visualize how this works, but there's potentially some confusion about "loose ends."
Think about the following composition of a vine 3→3 with another 3→2 :
The composite vine has that funny little hair sticking out of the bottom right vertex that doesn't come from a top vertex anymore. What we do to make sense of this is just "contract" that hair down to nothing. We ignore it, i.e.:
I get that this may seem a bit arbitrary, but Lavers in the reference I cited above proves that it works out (at least when n=m, which gives you a monoid structure), and Weber gets into it for the more general case in section 6.3 of this: https://t.co/U9uSMBJkFS
I don't know if anyone says this in any of those references, but I imagine you can sort add an arbitrary number of "hairs" to any vine and they just kind of contract down. Like you could plug that into the definition somehow, but anyway I guess it doesn't matter.
So these are the morphisms of this category V. Notice that the braid group embeds into the endomorphism monoid V(n,n) (where the monoid structure comes from composition).
This category is also braided monoidal. The monoidal structure is given by addition of natural numbers. The braiding should be a symmetry n+m→m+n, and it's the same braiding you have in the free braided monoidal category (a braid as a vine). Here it is for 3+2→2+3:
So why does this category contain a commutative monoid? Just like FinSet, the commutative monoid is going to be the object 1. There's a vine that looks like a Y that goes 1⊗1=2→1 and that's the multiplication. Why is it commutative?
Well, the twist map in this case is the braid 2→2 which just crosses the left strand over the right strand. And we want to ask that that diagram way up there (the first one in this thread) commutes, which just means that the two following braids should be the same vine:
But of course... that's exactly the funny condition we had way up there about isotoping vines. But I do think this is super cool, that there's this confluence of a sort-of "geometric" structure and a "categorical" structure.
And so if you take a braided monoidal functor out of this into a braided monoidal category it has to preserve the multiplication (the Y vine) and the braiding (the, you know, braid), and it has to preserve that commutative diagram. So it has to take 1 to a commutative monoid.
And just like with FinSet, that's ALL it does. It picks out a commutative diagram. So this isn't a proof at all, but hopefully you can sort of see why this category V is the free braided monoidal category containing a commutative monoid.
Now here's where things get "hypothetical" in the sense that I haven't written the proofs.
I want to say that braided monoidal pseudofunctors out of V into the 2-category of categories (where the "braided" monoidal structure is just Cartesian product) are equivalent to small braided monoidal categories.
I think that proving this is basically a matter of checking a bunch of technical details, but I haven't done it yet.
Here's the rough idea, and it goes back to the diagram that I've now drawn like three times, the braiding composed with the multiplication vs. the multiplication alone. In V these two morphisms are equal.
If you'll let me write X for the braid 2→2 that we've been discussing, then in V we have that YX=Y. But since we're now talking about pseudofunctors, we don't need composition to be preserved strictly.
In other words, all we need is an invertible natural transformation from F(YX) to F(Y). And that's EXACTLY the salient data of a braided monoidal category.
So I think this is pretty cool that this funny kind of combinatorial category is precisely the thing that "parameterizes" braided monoidal categories, and that the really important stuff about it has actually been floating around since the mid 90's!
Ultimately I think I just want people to think a bit more about this category. In some sense this category V is "as important" as these other really fundamental categories like FinSet and Δ, but people just never seem to have heard of it.
By the way, if you're, I dunno, some rich person reading this, you can give me money for explaining these fun things to you: https://t.co/S78AAkpD5j (as always if you're a grad student or postdoc who gives me money I'll find you and beat you up, so don't do it).
Credits: thread composed using @chirrapp, that commutative diagram was made using @q_uiver_app, and I'm about to produce a single document containing this thread by asking @threadreaderapp to unroll it.

More from Maths

Michael Kinyon
Michael Kinyon
@ProfKinyon
Loops and their multiplication groups

A thread in 15 parts

(0/15)

Recall that a quasigroup (Q,*) is a set Q with a binary operation * such that for each a,b in Q, the equations a*x=b and y*a=b have unique solutions x,y. Groups are quasigroups and this property is usually one of the first things proved in elementary group theory.

(1/15)

Note that we don't assume associativity of *!

A loop is a quasigroup with an identity element. The story of why they are called loops is an interesting one and may even be true, but I will save it for another day. I am going to focus on loops in this thread.

(2/15)

Natural examples of nonassociative loops:
- The nonzero octonions under multiplication
- The sphere S^7 under octonion multiplication
- I have discussed other examples


For each x in a loop Q, define the left & right translations L_x, R_x : Q->Q by L_x(y)=xy and R_x(y)=yx. These mappings are permutations of Q. The composition L_x L_y of two left translations is not necessarily a left translation because Q is not necessarily associative.

(4/15)
MATHS
P. Geerkens \u271d\ufe0f
P. Geerkens ✝️...
@pgeerkens
@GWOMaths One might say that physicists study the symmetry of nature, while mathematicians study the nature of symmetry.

1/

Observing symmetry in nature, such as noting the similarity between the symmetries of a snowflake and a hexagon, is readily comprehensible. What does it mean then to study "the nature of symmetry"?

2/

Mathematicians define a "group", G, as a set of elements {a,b,c, ...} with a binary operation ⊡ and a distinguished element e (the identity of G) satisfying these specific properties:

3/

For all a, b, c in G
1) Closure: a⊡b is in G.
2) Associativity: (a⊡b)⊡c = a⊡(b⊡c)
3) Identity: e⊡a = a⊡e = a.
4) Inverse: There exists an element a* such that a*⊡a = a⊡a* = e.

4/

Just as functions on the integers, rationals, or reals are defined as mappings, mathematicians define a *group morphism* μ as a mapping from one group to another that preserves the group structure:

5/
MATHS
Advertisement
Sleepless in Broadacres \u26d4\ufe0f
Sleepless in Broadacre...
@tesssulaman
IS HISTORY ALL TRUE SERIES: when even the #Calendar isn’t❓

THE REAL ACTUAL SOLAR CALENDAR:
*Based on the noble science of #Astronomy; the sister science to #Geometry, #Mathematics and the “almost” lost numerical science mysteries. Which was mastered in

“ancient” times, but is close to forgotten, in these “modern” days. Go figure❗️😄☦️

Navigation of the oceans was man’s first real great step of personal evolution, here on earth. The earliest of discovered sciences; #astronomy; allowed men to navigate through

routes to known territories; or to discover new ones, by the endlessly reliable positions of the stars and constellations, in the night sky. Hence; much diligent study, over who knows how many epochs, and great civilizations; was an esteemed scholarly pursuit. And led to a vast

understanding of the mechanics of our solar system, as well as the natural cycles of our planet, that even we; in this so-called Information Age “high civilization, don’t often know even exists any longer. A decay of common knowledge, in our “modern” educations, actually.

#Calendars have come and gone In the last few thousand years; motivated apparently by the politics of the day, or personal whim even, by the rulers of the moment; which somehow stuck, from there, and has hardly ever been questioned again.
SOCIETY , MATHS
Gro-Tsen
Gro-Tsen
@gro_tsen
OK, I may be guilty of a DoS attack attempt on mathematicians' brains here, so lest anyone waste too much precious brain time decoding this deliberately cryptic statement, let me do it for you. •1/15


First, as some asked, it is to be parenthesized as: “∀x.∀y.((∀z.((z∈x) ⇒ (((∀t.((t∈x) ⇒ ((t∈z) ⇒ (t∈y))))) ⇒ (z∈y)))) ⇒ (∀z.((z∈x) ⇒ (z∈y))))” (the convention is that ‘⇒’ is right-associative: “P⇒Q⇒R” means “P⇒(Q⇒R)”), but this doesn't clarify much. •2/15

Maybe we can make it a tad less abstruse by using guarded quantifiers (“∀u∈x.(…)” stands for “∀u.((u∈x)⇒(…))”): it is then “∀x.∀y.((∀z∈x.(((∀t∈x.((t∈z) ⇒ (t∈y)))) ⇒ (z∈y))) ⇒ (∀z∈x.(z∈y)))”. •3/15

Maybe a tad clearer again by writing “P(u)” for “u∈y” and leaving out the quantifier on y, viꝫ: “∀x.((∀z∈x.(((∀t∈x.((t∈z) ⇒ P(t)))) ⇒ P(z))) ⇒ (∀z∈x.P(z)))” [✯]. Now it appears as an induction principle: namely, … •4/15

… “in order to prove P(z) for all z∈x, we can assume, when proving P(z), that P(t) is already known for all t∈z∩x” (n.b.: “(∀z.(Q(z)⇒P(z)))⇒(∀z.P(z))” can be read “in order to prove P(z) for all z, we can assume Q(z) known when proving P(z)”). •5/15
MATHS
Riuji
Riuji
@weakconvergence
When I was starting out as a grad student, I remember being frustrated with analysis problems where it didn't use DIRECTLY the things we spent so much time proving in class.

As an example, let's look at a standard real analysis problem:

(1/23)


The problem looks like it can be done using the dominated convergence theorem.

This is an important theorem and is used in a lot of places outside a grad real analysis class. A student would go through a lot of buildup leading to this theorem.

(2/23)

Now, let's see whether the conditions for DCT are satisfied.

First, for fixed 00 as n->infinity.

So we have a.e. convergence of the integrand in [0,1].

To the student, this builds a stronger case to use DCT to solve the problem.

(3/23)

Finding an integrable dominating function is where the problem starts.

It would seem NATURAL (at least for me) to bound it with:

p.s. it feels "natural" to me because it is reminiscent of squeeze theorem problems, math students encounter in calculus.

(4/23)


However, 1/x^n is not integrable in (0,1) and hence cannot be (further) dominated by an integrable function.

So, what I would do is since I know it converges a.e. to 1, maybe it converges uniformly to 1?

This leads me into a BAD detour.

(5/23)
MATHS

You May Also Like

\u0b85\u0ba9\u0bcd\u0baa\u0bc6\u0bb4\u0bbf\u0bb2\u0bcd
அன்பெழில்...
@anbezhil12
#ஆதித்தியஹ்ருதயம் ஸ்தோத்திரம்
இது சூரிய குலத்தில் உதித்த இராமபிரானுக்கு தமிழ் முனிவர் அகத்தியர் உபதேசித்ததாக வால்மீகி இராமாயணத்தில் வருகிறது. ஆதித்ய ஹ்ருதயத்தைத் தினமும் ஓதினால் பெரும் பயன் பெறலாம் என மகான்களும் ஞானிகளும் காலம் காலமாகக் கூறி வருகின்றனர். ராம-ராவண யுத்தத்தை


தேவர்களுடன் சேர்ந்து பார்க்க வந்திருந்த அகத்தியர், அப்போது போரினால் களைத்து, கவலையுடன் காணப்பட்ட ராமபிரானை அணுகி, மனிதர்களிலேயே சிறந்தவனான ராமா போரில் எந்த மந்திரத்தைப் பாராயணம் செய்தால் எல்லா பகைவர்களையும் வெல்ல முடியுமோ அந்த ரகசிய மந்திரத்தை, வேதத்தில் சொல்லப்பட்டுள்ளதை உனக்கு

நான் உபதேசிக்கிறேன், கேள் என்று கூறி உபதேசித்தார். முதல் இரு சுலோகங்கள் சூழ்நிலையை விவரிக்கின்றன. மூன்றாவது சுலோகம் அகத்தியர் இராமபிரானை விளித்துக் கூறுவதாக அமைந்திருக்கிறது. நான்காவது சுலோகம் முதல் முப்பதாம் சுலோகம் வரை ஆதித்ய ஹ்ருதயம் என்னும் நூல். முப்பத்தி ஒன்றாம் சுலோகம்

இந்தத் துதியால் மகிழ்ந்த சூரியன் இராமனை வாழ்த்துவதைக் கூறுவதாக அமைந்திருக்கிறது.
ஐந்தாவது ஸ்லோகம்:
ஸர்வ மங்கள் மாங்கல்யம் ஸர்வ பாப ப்ரநாசனம்
சிந்தா சோக ப்ரசமனம் ஆயுர் வர்த்தனம் உத்தமம்
பொருள்: இந்த அதித்ய ஹ்ருதயம் என்ற துதி மங்களங்களில் சிறந்தது, பாவங்களையும் கவலைகளையும்


குழப்பங்களையும் நீக்குவது, வாழ்நாளை நீட்டிப்பது, மிகவும் சிறந்தது. இதயத்தில் வசிக்கும் பகவானுடைய அனுக்ரகத்தை அளிப்பதாகும்.
முழு ஸ்லோக லிங்க் பொருளுடன் இங்கே உள்ளது https://t.co/Q3qm1TfPmk
சூரியன் உலக இயக்கத்திற்கு மிக முக்கியமானவர். சூரிய சக்தியால்தான் ஜீவராசிகள், பயிர்கள்
ALL
(\u3063\u25d4\u25e1\u25d4)\u3063 \U0001f499 \U0001d440\U0001d4b6rymo Belfast \U0001f499\U0001f331\U0001f340 \u24cb\U0001f397\ufe0f
(っ◔◡◔)っ 💙 𝑀𝒶rymo Belfa...
@MarymoBelfast
THREAD PART 1.

On Sunday 21st June, 14 year old Noah Donohoe left his home to meet his friends at Cave Hill Belfast to study for school. #RememberMyNoah💙


He was on his black Apollo mountain bike, fully dressed, wearing a helmet and carrying a backpack containing his laptop and 2 books with his name on them. He also had his mobile phone with him.

On the 27th of June. Noah's naked body was sadly discovered 950m inside a storm drain, between access points. This storm drain was accessible through an area completely unfamiliar to him, behind houses at Northwood Road. https://t.co/bpz3Rmc0wq


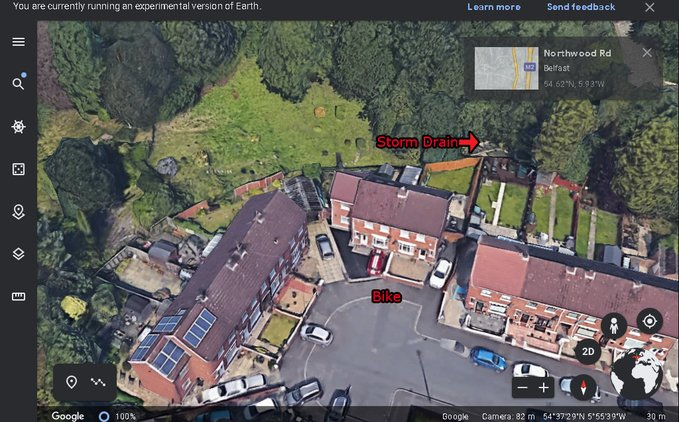
"Noah's body was found by specially trained police officers between two drain access points within a section of the tunnel running under the Translink access road," said Mr McCrisken."

Noah's bike was also found near a house, behind a car, in the same area. It had been there for more than 24 hours before a member of public who lived in the street said she read reports of a missing child and checked the bike and phoned the police.
CRIME
Advertisement
RadioChinar
RadioChinar
@RadioChinar
Demystifying Ghazwa-e-Hind. A #thread.

A recent video of Shoaid Akhter surfaced in social media creating a lot of controversy where the #Pakistani Cricketer can be seen suggesting invasion of India by using the term Ghazwa-e-Hind.
Radicalization of sportsmen seen off late
(1/10)


Some radical Islamic preachers believes that Ghazwa-e-Hind means a “Holy War against India”. As per this irrational & profane concept, there will be a fierce battle to secure victory over #India.
#Kashmir
(2/10)


#Pakistan-based terror groups, like JeM have been using Ghazwa-e-Hind as a Hadith to recruit, fund and justify its terror strikes as a religious holy war against #India.
#Kashmir
(3/10)


Some machiavellian people claim it is a prophecy that Muslim warriors will wage war against the #India.
Jaish & others falsely propagate that Jihad against India is considered holy in Islam & that those participating in it will be granted an easy entry into paradise.
(4/10)


However prolific scholars says that this is a made-up interpretation of some verse in The Holy Quran to mislead the gullible youth of #Pakistan into picking up arms and fighting its Army's personal battle against #India.
#Kashmir
(5/10)
SOCIETY
Anu Satheesh \U0001f1ee\U0001f1f3
Anu Satheesh 🇮🇳...
@AnuSatheesh5
Neyyattinkara Krishna Kshetram
#Thiruvananthapuram
#KeralaTemples 🚩

Neyyattinkara Krishna Kshetram is considered as the Guruvayur of Trivandrum. Thrikkayyil Venna (butter) is main offering to Neyyattinkara Unnikannan. Kshetram is supposed to be built by Marthanda Varma.


Sthala Puranam says that, Anizham Thirunal Marthanda Varma was surrounded by his enemies, Ettuveettil Pillamar, while he was near the place where Temple is situated now. The king prayed to Padmanabhaswamy to protect him.  At that time, a small boy was seen there and he


advised the king to hide himself inside the hollow trunk of a jack fruit tree. The king was surprised to find a small boy in the forest, but agreed to the advice
Thus he was saved from the attack. When the enemies left, king tried to know about the boy, but he couldn't.


He believed that it was krishna himself who saved his life. A temple was built here, which is the present Neyyattinkara Krishna Kshetram. The jack fruit tree where  the king hid himself is now known as Ammachi Plavu. Ashtami Rohini, Vishu are very famous here

Hare Krishna
🙏🕉🙏
ALL
Lindsey Simmons
Lindsey Simmons
@LynzforCongress
Joshua Hawley, Missouri's Junior Senator, is an autocrat in waiting.

His arrogance and ambition prohibit any allegiance to morality or character.

Thus far, his plan to seize the presidency has fallen into place.

An explanation in photographs.

🧵

Joshua grew up in the next town over from mine, in Lexington, Missouri. A a teenager he wrote a column for the local paper, where he perfected his political condescension.

2/


By the time he reached high-school, however, he attended an elite private high-school 60 miles away in Kansas City.

This is a piece of his history he works to erase as he builds up his counterfeit image as a rural farm boy from a small town who grew up farming.

3/


After graduating from Rockhurst High School, he attended Stanford University where he wrote for the Stanford Review--a libertarian publication founded by Peter Thiel..

4/

(Full Link: https://t.co/zixs1HazLk)


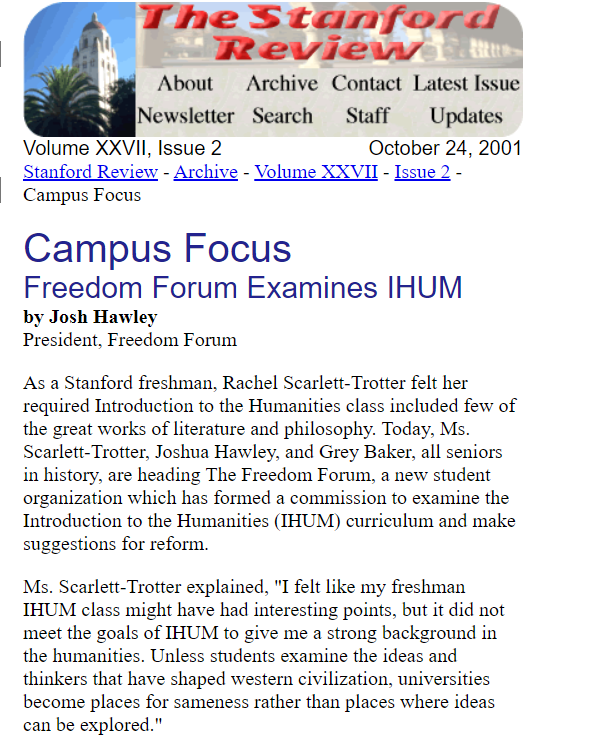
Hawley's writing during his early 20s reveals that he wished for the curriculum at Stanford and other "liberal institutions" to change and to incorporate more conservative moral values.

This led him to create the "Freedom Forum."

5/
HISTORY