To my JVM friends looking to explore Machine Learning techniques - you don’t necessarily have to learn Python to do that. There are libraries you can use from the comfort of your JVM environment. 🧵👇
More from Data science
1/ A ∞-wide NN of *any architecture* is a Gaussian process (GP) at init. The NN in fact evolves linearly in function space under SGD, so is a GP at *any time* during training. https://t.co/v1b6kndqCk With Tensor Programs, we can calculate this time-evolving GP w/o trainin any NN
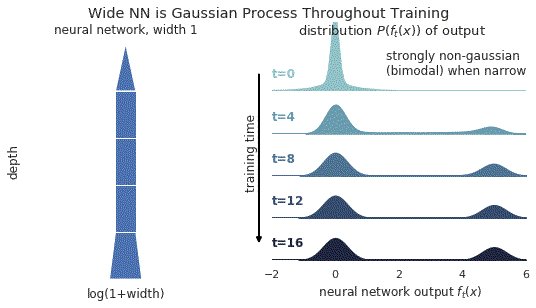
2/ In this gif, narrow relu networks have high probability of initializing near the 0 function (because of relu) and getting stuck. This causes the function distribution to become multi-modal over time. However, for wide relu networks this is not an issue.
3/ This time-evolving GP depends on two kernels: the kernel describing the GP at init, and the kernel describing the linear evolution of this GP. The former is the NNGP kernel, and the latter is the Neural Tangent Kernel (NTK).
4/ Once we have these two kernels, we can derive the GP mean and covariance at any time t via straightforward linear algebra.
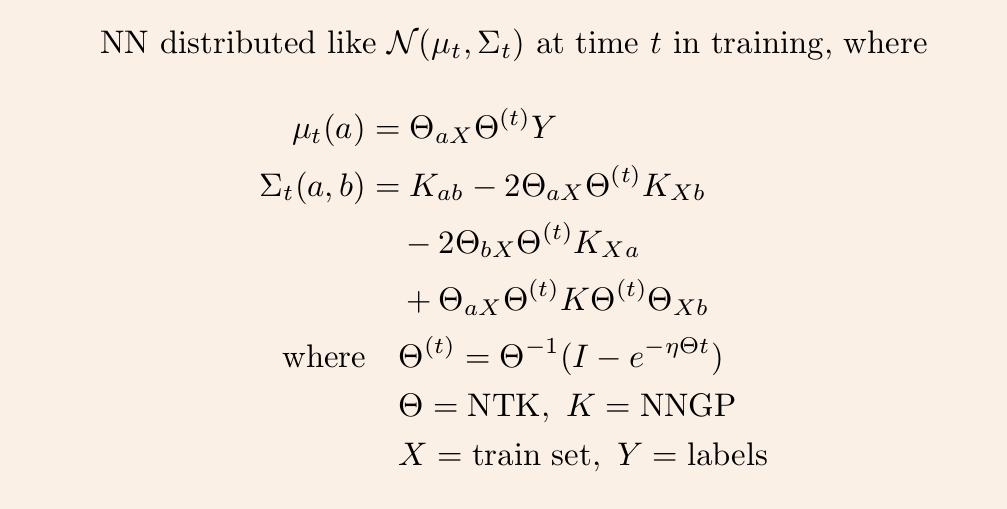
5/ So it remains to calculate the NNGP kernel and NT kernel for any given architecture. The first is described in https://t.co/cFWfNC5ALC and in this thread

2/ In this gif, narrow relu networks have high probability of initializing near the 0 function (because of relu) and getting stuck. This causes the function distribution to become multi-modal over time. However, for wide relu networks this is not an issue.
3/ This time-evolving GP depends on two kernels: the kernel describing the GP at init, and the kernel describing the linear evolution of this GP. The former is the NNGP kernel, and the latter is the Neural Tangent Kernel (NTK).
4/ Once we have these two kernels, we can derive the GP mean and covariance at any time t via straightforward linear algebra.
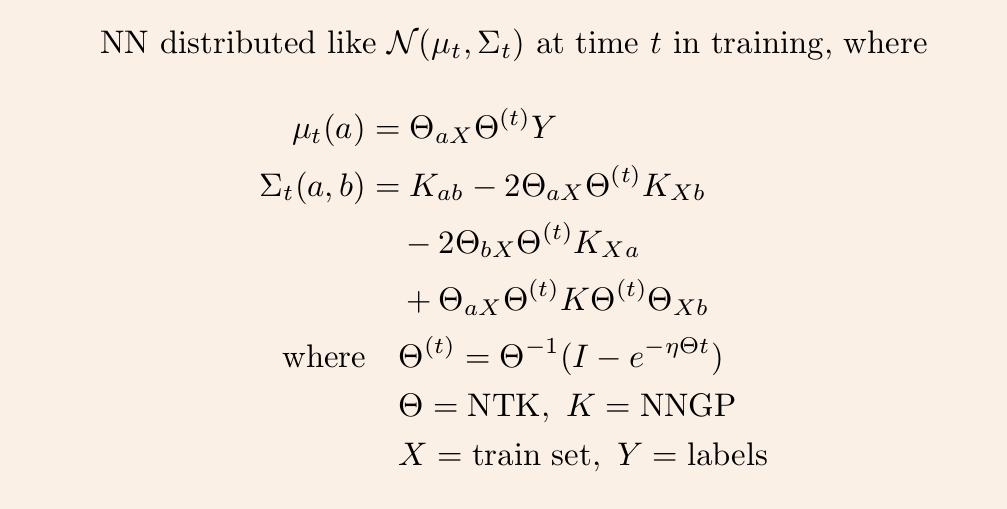
5/ So it remains to calculate the NNGP kernel and NT kernel for any given architecture. The first is described in https://t.co/cFWfNC5ALC and in this thread
✨✨ BIG NEWS: We are hiring!! ✨✨
Amazing Research Software Engineer / Research Data Scientist positions within the @turinghut23 group at the @turinginst, at Standard (permanent) and Junior levels 🤩
👇 Here below a thread on who we are and what we
We are a highly diverse and interdisciplinary group of around 30 research software engineers and data scientists 😎💻 👉 https://t.co/KcSVMb89yx #RSEng
We value expertise across many domains - members of our group have backgrounds in psychology, mathematics, digital humanities, biology, astrophysics and many other areas 🧬📖🧪📈🗺️⚕️🪐
https://t.co/zjoQDGxKHq
/ @DavidBeavan @LivingwMachines
In our everyday job we turn cutting edge research into professionally usable software tools. Check out @evelgab's #LambdaDays 👩💻 presentation for some examples:
We create software packages to analyse data in a readable, reliable and reproducible fashion and contribute to the #opensource community, as @drsarahlgibson highlights in her contributions to @mybinderteam and @turingway: https://t.co/pRqXtFpYXq #ResearchSoftwareHour
Amazing Research Software Engineer / Research Data Scientist positions within the @turinghut23 group at the @turinginst, at Standard (permanent) and Junior levels 🤩
👇 Here below a thread on who we are and what we
We are a highly diverse and interdisciplinary group of around 30 research software engineers and data scientists 😎💻 👉 https://t.co/KcSVMb89yx #RSEng
We value expertise across many domains - members of our group have backgrounds in psychology, mathematics, digital humanities, biology, astrophysics and many other areas 🧬📖🧪📈🗺️⚕️🪐
https://t.co/zjoQDGxKHq
/ @DavidBeavan @LivingwMachines
In our everyday job we turn cutting edge research into professionally usable software tools. Check out @evelgab's #LambdaDays 👩💻 presentation for some examples:
We create software packages to analyse data in a readable, reliable and reproducible fashion and contribute to the #opensource community, as @drsarahlgibson highlights in her contributions to @mybinderteam and @turingway: https://t.co/pRqXtFpYXq #ResearchSoftwareHour
Wellll... A few weeks back I started working on a tutorial for our lab's Code Club on how to make shitty graphs. It was too dispiriting and I balked. A twitter workshop with figures and code:
Here's the code to generate the data frame. You can get the "raw" data from https://t.co/jcTE5t0uBT

Obligatory stacked bar chart that hides any sense of variation in the data

Obligatory stacked bar chart that shows all the things and yet shows absolutely nothing at the same time

STACKED Donut plot. Who doesn't want a donut? Who wouldn't want a stack of them!?! This took forever to render and looked worse than it should because coord_polar doesn't do scales="free_x".

When are you doing pie charts?
— #BlackLivesMatter (@surt_lab) October 13, 2020
Here's the code to generate the data frame. You can get the "raw" data from https://t.co/jcTE5t0uBT

Obligatory stacked bar chart that hides any sense of variation in the data

Obligatory stacked bar chart that shows all the things and yet shows absolutely nothing at the same time

STACKED Donut plot. Who doesn't want a donut? Who wouldn't want a stack of them!?! This took forever to render and looked worse than it should because coord_polar doesn't do scales="free_x".

You May Also Like
THREAD PART 1.
On Sunday 21st June, 14 year old Noah Donohoe left his home to meet his friends at Cave Hill Belfast to study for school. #RememberMyNoah💙

He was on his black Apollo mountain bike, fully dressed, wearing a helmet and carrying a backpack containing his laptop and 2 books with his name on them. He also had his mobile phone with him.
On the 27th of June. Noah's naked body was sadly discovered 950m inside a storm drain, between access points. This storm drain was accessible through an area completely unfamiliar to him, behind houses at Northwood Road. https://t.co/bpz3Rmc0wq
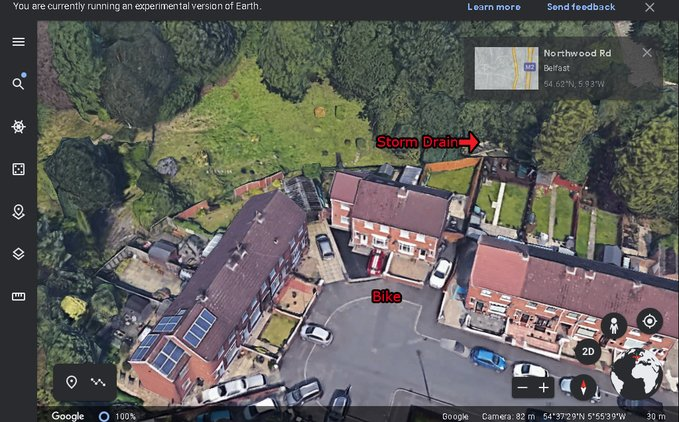
"Noah's body was found by specially trained police officers between two drain access points within a section of the tunnel running under the Translink access road," said Mr McCrisken."
Noah's bike was also found near a house, behind a car, in the same area. It had been there for more than 24 hours before a member of public who lived in the street said she read reports of a missing child and checked the bike and phoned the police.
On Sunday 21st June, 14 year old Noah Donohoe left his home to meet his friends at Cave Hill Belfast to study for school. #RememberMyNoah💙

He was on his black Apollo mountain bike, fully dressed, wearing a helmet and carrying a backpack containing his laptop and 2 books with his name on them. He also had his mobile phone with him.
On the 27th of June. Noah's naked body was sadly discovered 950m inside a storm drain, between access points. This storm drain was accessible through an area completely unfamiliar to him, behind houses at Northwood Road. https://t.co/bpz3Rmc0wq

"Noah's body was found by specially trained police officers between two drain access points within a section of the tunnel running under the Translink access road," said Mr McCrisken."
Noah's bike was also found near a house, behind a car, in the same area. It had been there for more than 24 hours before a member of public who lived in the street said she read reports of a missing child and checked the bike and phoned the police.


















