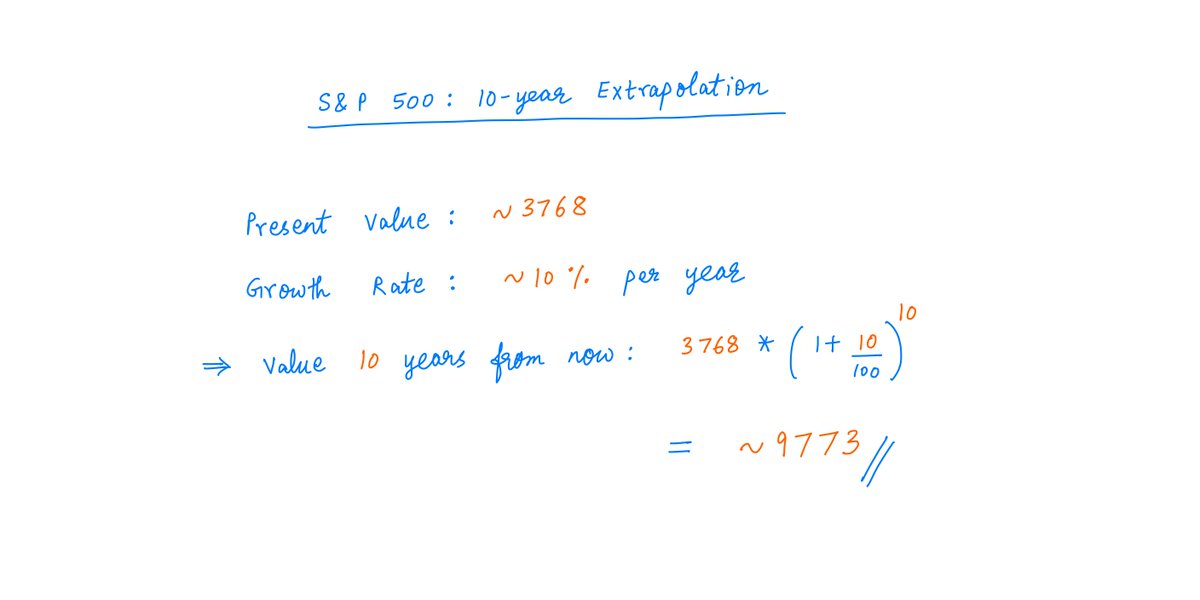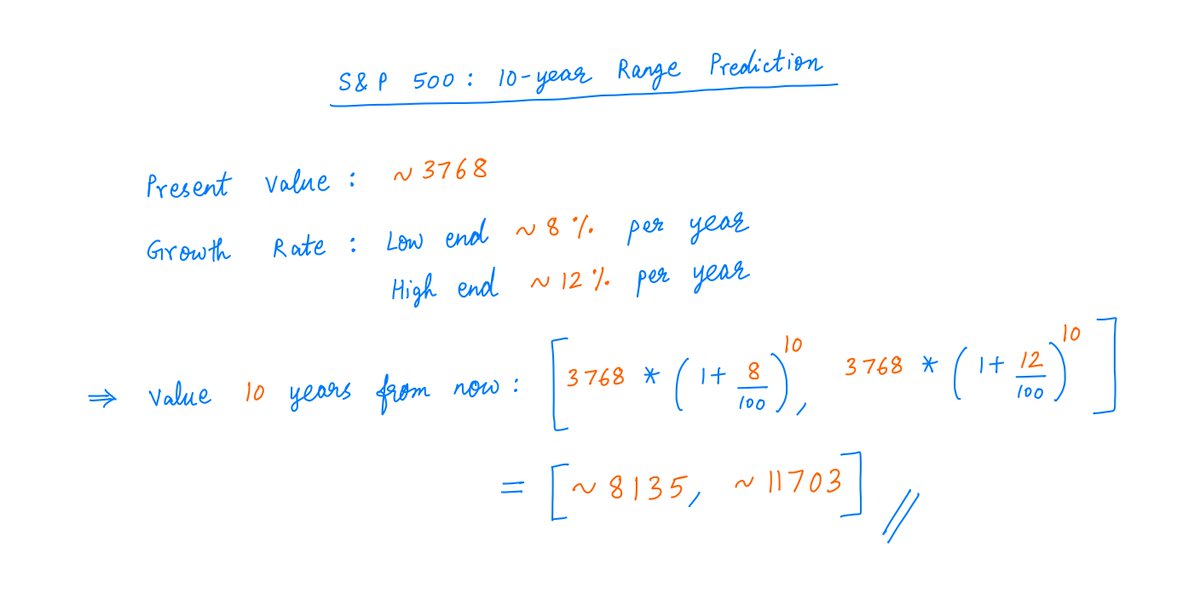2/
The S&P 500 index is at ~3768 today.
Suppose we want to predict where it will be 10 years from now.
Historically, we know that this index has returned ~10% per year.
If we simply extrapolate this, we get an estimate of ~9773 for the index 10 years from now:
3/
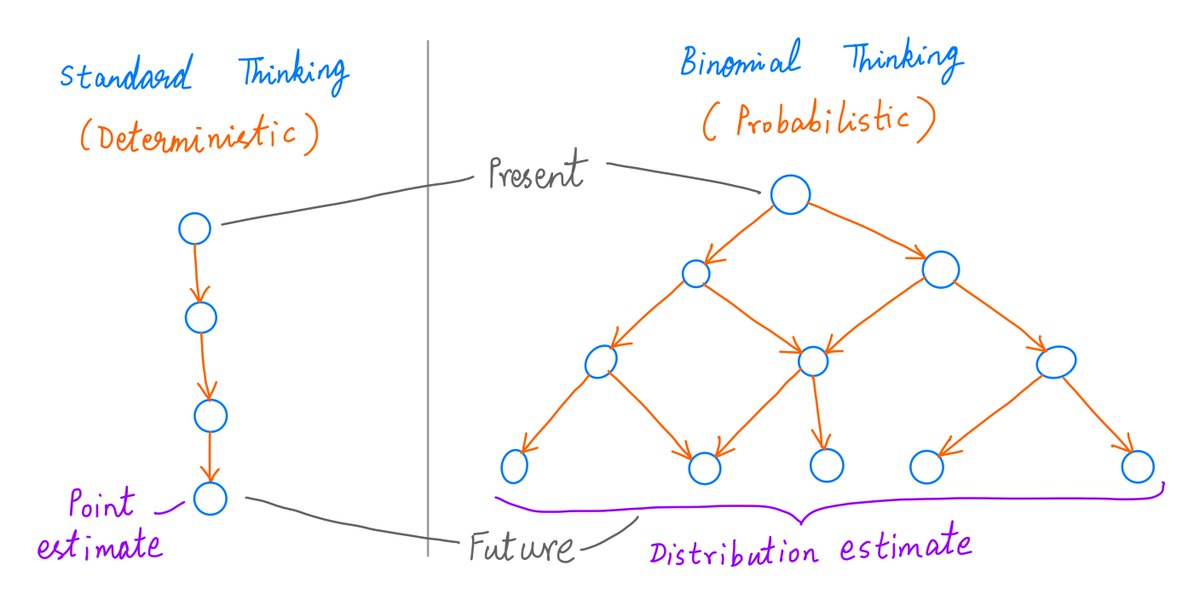
What we just did is called a "point estimate" -- a prediction about the future that's a single number (9773).
But of course, we know the future is uncertain. It's impossible to predict it so precisely.
So, there's a sense of *false precision* in point estimates like this.
4/
To emphasize the uncertainty inherent in such predictions, a better approach is to predict a *range* of values rather than a single number.
For example, we may say the index will return somewhere in the *range* of 8% to 12% (instead of a fixed 10%) per year.
5/
10 years from now, this implies an index value in the *range* [8135, 11703]:
6/
A range is more nuanced than a point estimate, but we still have a problem:
Range estimates tell us nothing about the relative likelihoods of different parts of the range.
For example, which is more likely -- the low end or high end of the range? We don't know.
7/
Ideally, we want to say something like:
10 years from now, there's a ~93% chance that the index will lie in the range [5648, 15244], and there are 60/40 odds favoring the bottom half of this range.
Binomial thinking enables us to make such *probabilistic* predictions.
8/
With binomial thinking, we can derive not just a *range* of possible outcomes, but also the *probability* of seeing each outcome in this range.
It's easiest to illustrate this with an example.
9/
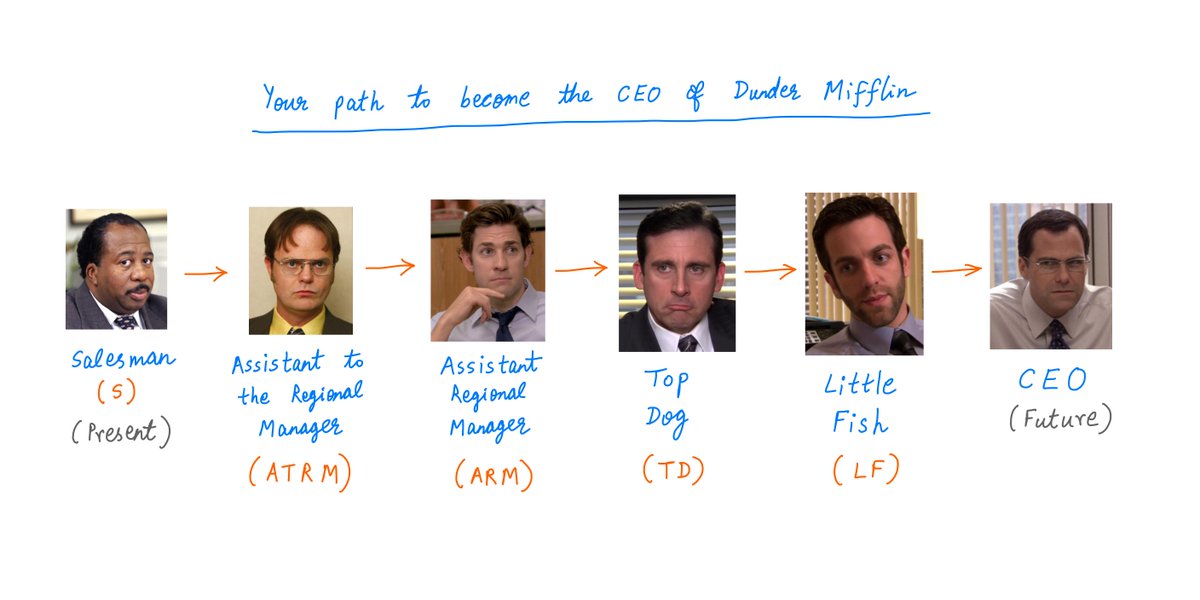
Imagine that you just joined the Dunder Mifflin Paper Company as a Salesman.
From these humble beginnings, you hope to rise quickly within the organization.
You want to become the CEO in 6 years time.
Here's your path to the top job:
10/
So, you need 5 promotions to become the CEO.
Let's say you come up for a promotion every year.
And every year, there's a 75% chance you'll get the promotion (and a 25% chance you won't).
So, what's the probability that you'll achieve your goal of becoming CEO in 6 years?
11/
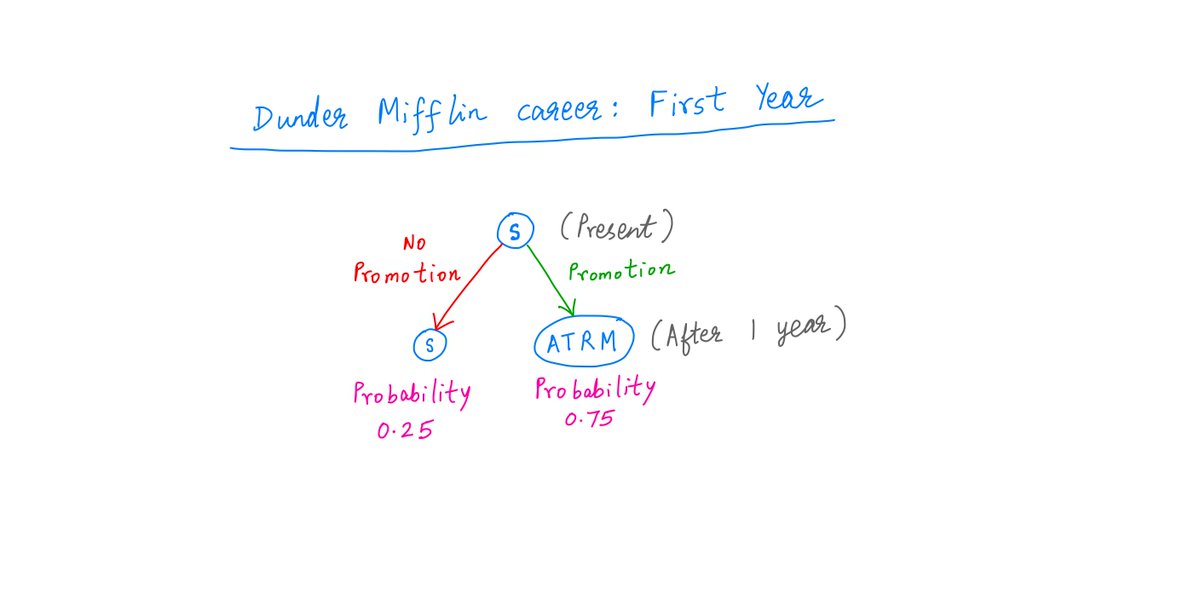
Let's tackle this one year at a time.
At the end of your first year on the job, you come up for a promotion.
If you get it, you become Assistant To the Regional Manager (ATRM). If not, you remain Salesman (S). The odds are 75/25.
12/
So, at the end of Year 1, there are 2 possible states you could be in: S (Salesman) and ATRM (Assistant To the Regional Manager).
S has a 25% probability and ATRM has a 75% probability.
13/
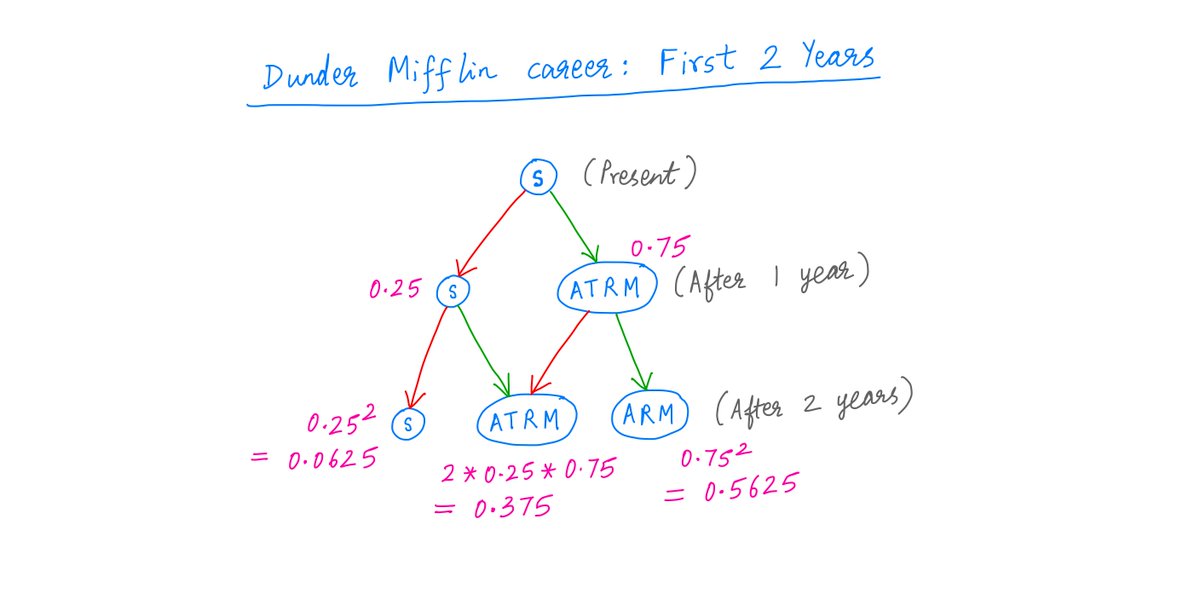
Similarly, at the end of Year 2, you again come up for a promotion.
Depending on whether you get it, there are now 3 possible states you could be in: S, ATRM, and ARM.
Again, each state has a probability (in pink below):
14/
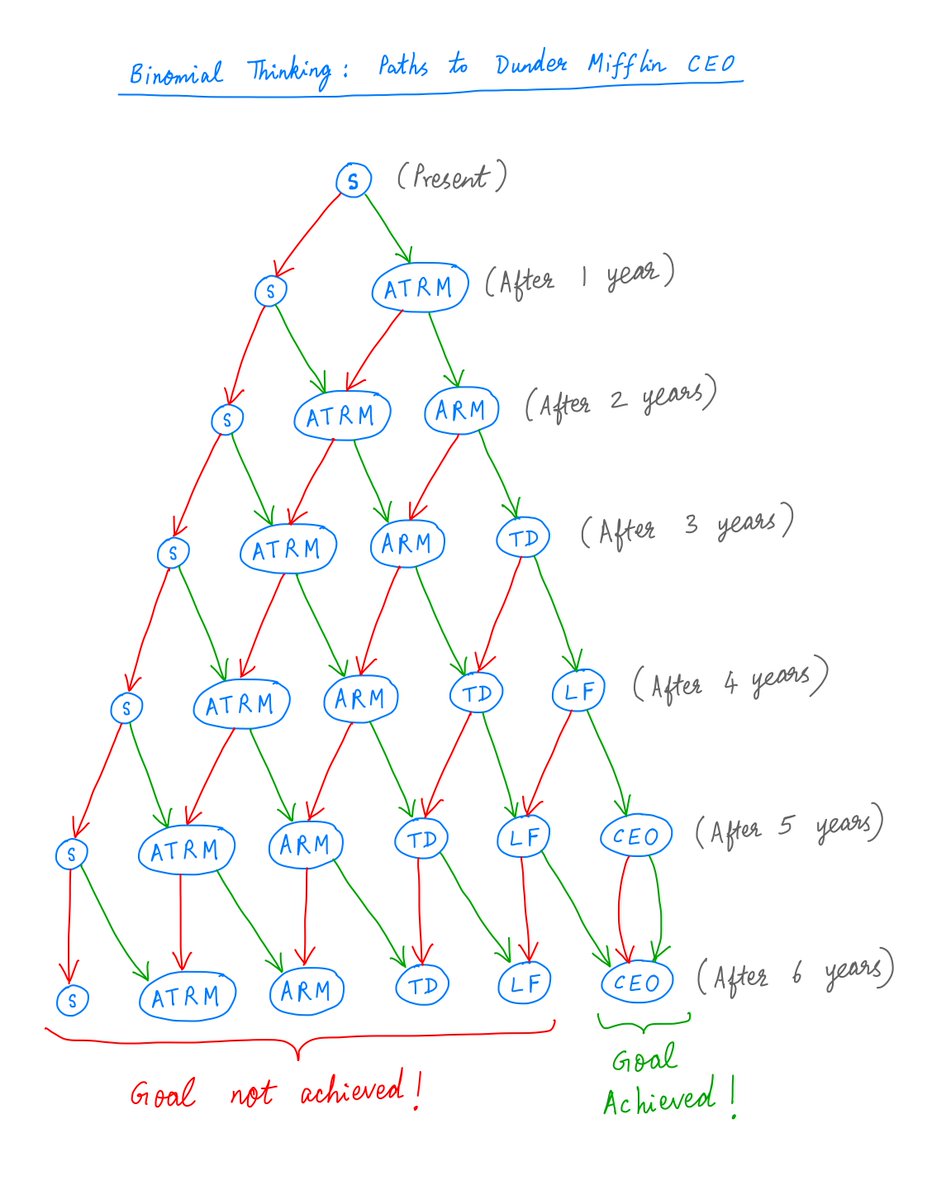
Continuing this way, we can draw up all the career trajectories you can possibly follow during your first 6 years at Dunder Mifflin.
In some of these trajectories, you achieve your goal of becoming CEO. In others, you don't.
15/
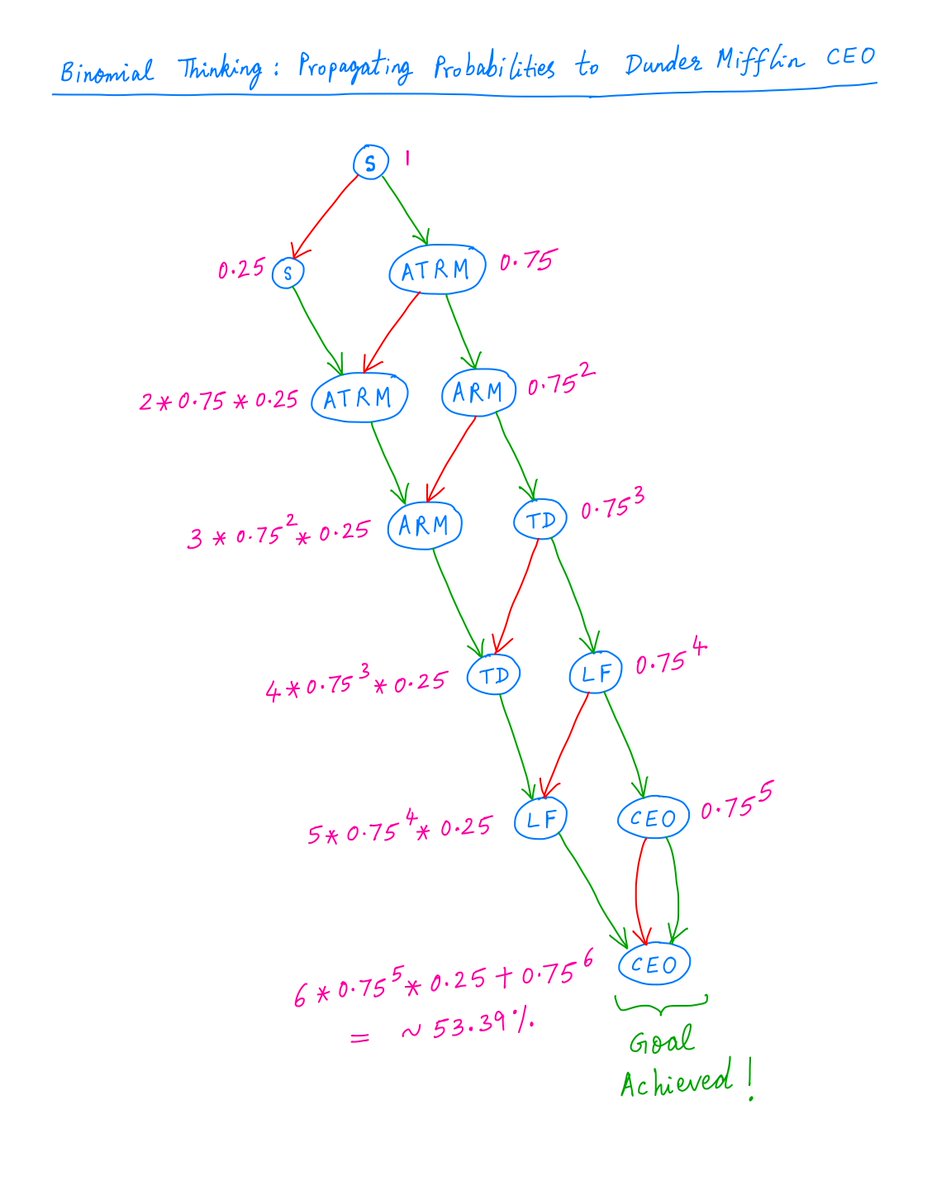
And by simply propagating the 75/25 probabilities all the way down, we find that your probability of becoming CEO within 6 years is ~53.39%:
16/
This example illustrates some key features of binomial thinking.
Feature 1. Break time into small chunks.
For example, in this case, we broke your first 6 years at Dunder Mifflin into 6 1-year chunks.
17/
Feature 2. At the end of each time chunk, figure out all possible states we can be in.
For example, at the end of Year 2 at Dunder Mifflin, your possible states are: S, ATRM, and ARM.
18/
Feature 3. At each possible state, consider 2 possible scenarios and where each one leads.
The scenarios could be getting a promotion or not. The S&P 500 going up or down. An election won by a Democrat or a Republican. A guilty or not guilty court verdict. Etc.
19/
Feature 4. Account for probabilities. Propagate them top-down through the binomial diagram to work out the chances of getting various desirable and undesirable outcomes.
20/
That's pretty much all there is to binomial thinking.
As you've seen, it's a simple way to incorporate chance events and probabilistic outcomes into our analyses.
It's particularly useful when simple point estimates and range estimates prove to be inadequate.
21/
But there are also drawbacks to binomial thinking.
For example, it advocates a binary worldview. At each state, we only account for 2 possible ways the future can unfold (eg, "promotion" vs "no promotion").
22/
But often, there are more than 2 ways.
For example, the S&P 500 may go down 30%, up 5%, up 25%, etc. The possibilities are endless, but binomial logic reduces them to just 2.
Also, in many situations, the binomial diagram becomes pretty big -- and hard to analyze.
23/
But even with these drawbacks, binomial thinking is a definite step up over standard deterministic thinking.
In the land of the blind, the one-eyed man is king.
In the land of point estimators, the binomial thinker is king.
24/
Many financial calculations rely on binomial thinking. Examples include the binomial options pricing model and its cousin Black-Scholes.
Also, this paper by
@mjmauboussin uses binomial thinking to value the "optionality" of businesses:
https://t.co/3pn0oAWh0H
25/
At every tweet of this thread, you had a binary choice: you could continue reading, or you could skip the rest of the thread.
You're that special person who elected to continue 25 times in a row. A binomial wonder.
Thank you so much!
Have a great weekend.
/End