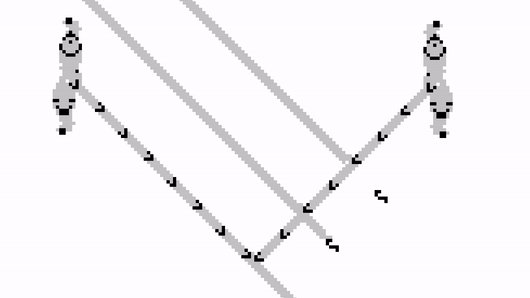
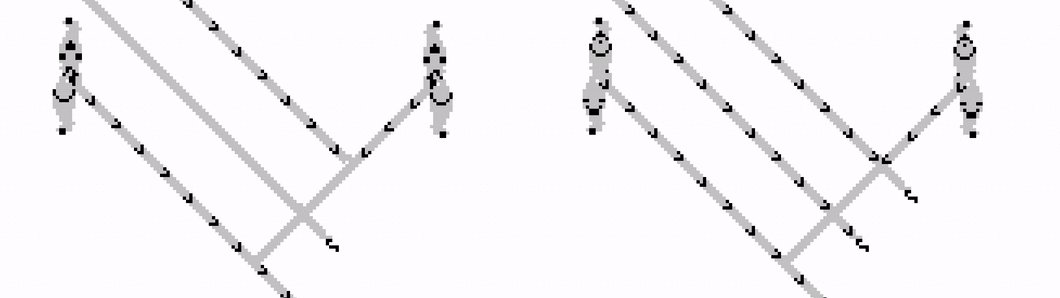So, let's see how the 𝗔𝗡𝗗, 𝗢𝗥 and 𝗡𝗢𝗧 gates can actually be constructed in Conway's Game of Life...
Fifty years have passed since CONWAY'S GAME OF LIFE firstly appeared on a column called "Mathematical Games" on @sciam.
While most Programmers & Computer Science enthusiasts are familiar with it, not many know that the game is actually TURING COMPLETE.
Let's see why. ⠠⠵
🧵👇

So, let's see how the 𝗔𝗡𝗗, 𝗢𝗥 and 𝗡𝗢𝗧 gates can actually be constructed in Conway's Game of Life...
One very popular choice is to use a stream of GLIDERS. The so-called GOSPER GLIDER GUN can generated a new glider every 30 generations. 🔫
Hence, receiving a glider every 30 generations counts as a "1".

This means that a GLIDER GUN can stop an incoming glider stream!
We can exploit this mechanism to simulate a NOT gate:
⬇️ 𝗡𝗢𝗧 0 = 1 ⬇️ 𝗡𝗢𝗧 1 = 0
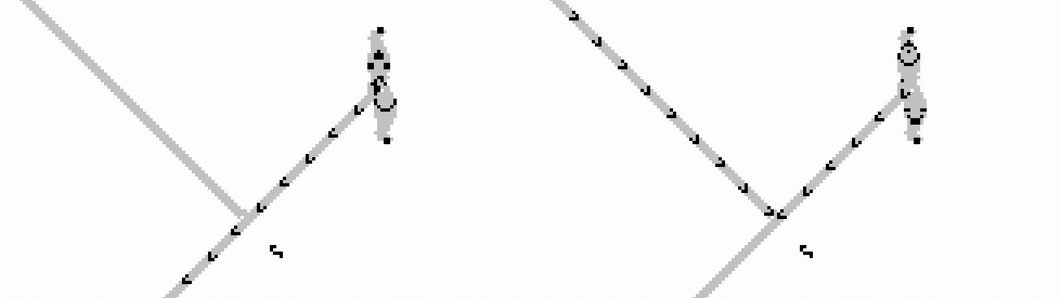
⬇️ 0 𝗔𝗡𝗗 1 = 0 ⬇️ 1 𝗔𝗡𝗗 0 = 0

⬇️ 1 𝗔𝗡𝗗 1 = 1
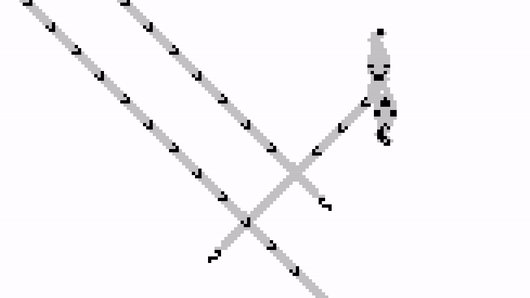
This is one step away from TURING COMPLETENESS. ✨
What we need is a memory block! The pattern below works as a SET-RESET LATCH: a simple 1-bit memory register!
If you are interested to learn more about this, this short documentary goes into great length to explain the process of building an actual computer in Conway's Game of Life. ⠠⠵
https://t.co/7e3LKmGfNi
More from Gaming
You May Also Like
The first area to focus on is diversity. This has become a dogma in the tech world, and despite the fact that tech is one of the most meritocratic industries in the world, there are constant efforts to promote diversity at the expense of fairness, merit and competency. Examples:
USC's Interactive Media & Games Division cancels all-star panel that included top-tier game developers who were invited to share their experiences with students. Why? Because there were no women on the
ElectronConf is a conf which chooses presenters based on blind auditions; the identity, gender, and race of the speaker is not known to the selection team. The results of that merit-based approach was an all-male panel. So they cancelled the conference.
Apple's head of diversity (a black woman) got in trouble for promoting a vision of diversity that is at odds with contemporary progressive dogma. (She left the company shortly after this
Also in the name of diversity, there is unabashed discrimination against men (especially white men) in tech, in both hiring policies and in other arenas. One such example is this, a developer workshop that specifically excluded men: https://t.co/N0SkH4hR35

USC's Interactive Media & Games Division cancels all-star panel that included top-tier game developers who were invited to share their experiences with students. Why? Because there were no women on the
ElectronConf is a conf which chooses presenters based on blind auditions; the identity, gender, and race of the speaker is not known to the selection team. The results of that merit-based approach was an all-male panel. So they cancelled the conference.
Apple's head of diversity (a black woman) got in trouble for promoting a vision of diversity that is at odds with contemporary progressive dogma. (She left the company shortly after this
Also in the name of diversity, there is unabashed discrimination against men (especially white men) in tech, in both hiring policies and in other arenas. One such example is this, a developer workshop that specifically excluded men: https://t.co/N0SkH4hR35