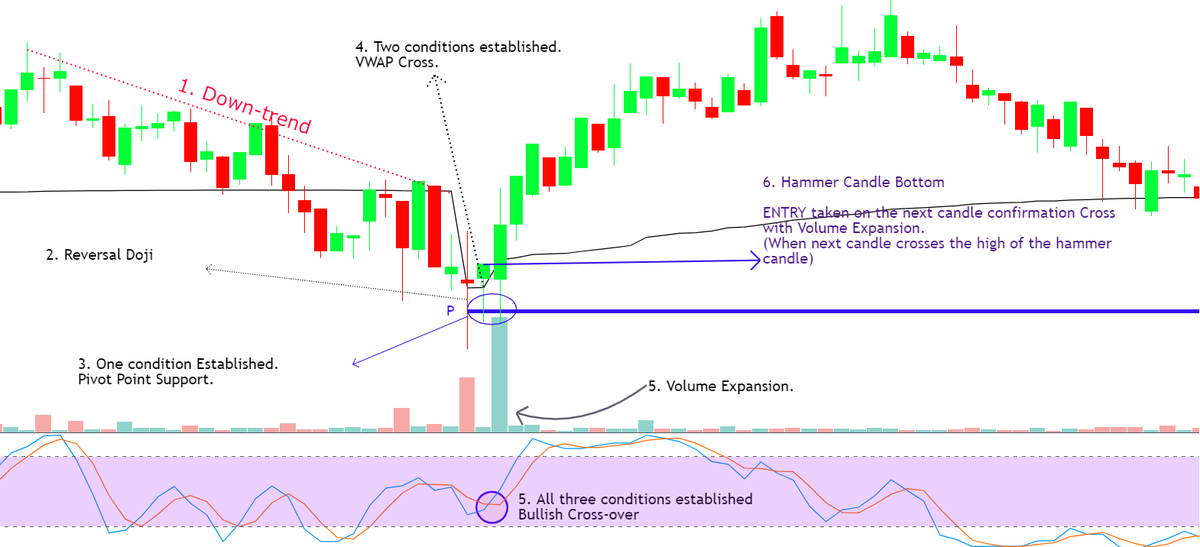
Suppose that for a given setup, price hits target before it reaches invalidation 70% of the time. Great, right? But getting filled is not guaranteed.
The more right you are about your trade setup, the less likely you are to get filled
By extension, getting filled actually lowers the Bayesian probability that you are right
Should I sacrifice some RRR to get filled more often?
The eternal dilemma of contrarian trading
Suppose that for a given setup, price hits target before it reaches invalidation 70% of the time. Great, right? But getting filled is not guaranteed.
Scenario 2: If only 40 out of 100 limits get filled, expected hit rate is 25%
Both scenarios have 30 losses in expectation, but the hit rate in the first is >2x better simply because more trades were taken
EV = hitrate * avg_win_R + (1-hitrate) * avg_loss_R
So we want argmax(EV), and we can compute this by seeing how hitrate and avg_win_R affect the EV of the setup.
Here's a real example where I completed this optimization.
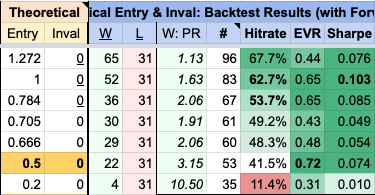
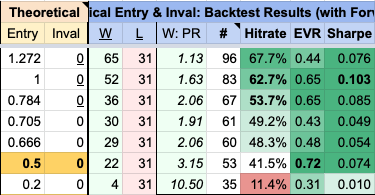
- the average win R tends to increase ("W:PR")
- the number of losses ("L") stays constant at 31
- but the number of trades taken decreases ("#")
- so the hit rate decreases, from a max of 67.7% to a min of 11.4%.
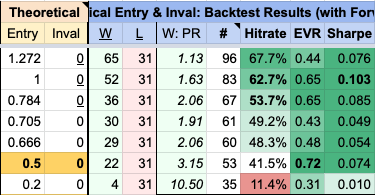
- Understand the tradeoff between RRR and hit rate. I talked about limit orders in this thread but a similar relationship applies to market entries too
- There are no easy answers here. Only the prospect of hard work collecting good data and learning from it.
💪
@Captain_Kole1 @melodyofrhythm @ape_rture @realadamli @7ommyZero @voicelessFvoice
More from Trading
A thread on getting intraday (any timeframe) data to excel without any coding. Limited to only last 60 days. Fetches from zerodha chart.
👇
1. Open the chart on zerodha web in chrome. Right click and select 'Inspect'. Click 'Network' as shown in this pic.
2. Right click on the last entry on the table you see and click 'copy as cURL (bash)'
3. Go to website https://t.co/f8rhwoGLUc and paste on the left box and click 'Run'
4. The output below candles written on right of box is the ohlc, volume and oi data. Copy and paste to excel.
👇
1. Open the chart on zerodha web in chrome. Right click and select 'Inspect'. Click 'Network' as shown in this pic.
2. Right click on the last entry on the table you see and click 'copy as cURL (bash)'
3. Go to website https://t.co/f8rhwoGLUc and paste on the left box and click 'Run'
4. The output below candles written on right of box is the ohlc, volume and oi data. Copy and paste to excel.
You May Also Like
I just finished Eric Adler's The Battle of the Classics, and wanted to say something about Joel Christiansen's review linked below. I am not sure what motivates the review (I speculate a bit below), but it gives a very misleading impression of the book. 1/x
The meat of the criticism is that the history Adler gives is insufficiently critical. Adler describes a few figures who had a great influence on how the modern US university was formed. It's certainly critical: it focuses on the social Darwinism of these figures. 2/x
Other insinuations and suggestions in the review seem wildly off the mark, distorted, or inappropriate-- for example, that the book is clickbaity (it is scholarly) or conservative (hardly) or connected to the events at the Capitol (give me a break). 3/x
The core question: in what sense is classics inherently racist? Classics is old. On Adler's account, it begins in ancient Rome and is revived in the Renaissance. Slavery (Christiansen's primary concern) is also very old. Let's say classics is an education for slaveowners. 4/x
It's worth remembering that literacy itself is elite throughout most of this history. Literacy is, then, also the education of slaveowners. We can honor oral and musical traditions without denying that literacy is, generally, good. 5/x
As someone\u2019s who\u2019s read the book, this review strikes me as tremendously unfair. It mostly faults Adler for not writing the book the reviewer wishes he had! https://t.co/pqpt5Ziivj
— Teresa M. Bejan (@tmbejan) January 12, 2021
The meat of the criticism is that the history Adler gives is insufficiently critical. Adler describes a few figures who had a great influence on how the modern US university was formed. It's certainly critical: it focuses on the social Darwinism of these figures. 2/x
Other insinuations and suggestions in the review seem wildly off the mark, distorted, or inappropriate-- for example, that the book is clickbaity (it is scholarly) or conservative (hardly) or connected to the events at the Capitol (give me a break). 3/x
The core question: in what sense is classics inherently racist? Classics is old. On Adler's account, it begins in ancient Rome and is revived in the Renaissance. Slavery (Christiansen's primary concern) is also very old. Let's say classics is an education for slaveowners. 4/x
It's worth remembering that literacy itself is elite throughout most of this history. Literacy is, then, also the education of slaveowners. We can honor oral and musical traditions without denying that literacy is, generally, good. 5/x
I’m torn on how to approach the idea of luck. I’m the first to admit that I am one of the luckiest people on the planet. To be born into a prosperous American family in 1960 with smart parents is to start life on third base. The odds against my very existence are astronomical.
I’ve always felt that the luckiest people I know had a talent for recognizing circumstances, not of their own making, that were conducive to a favorable outcome and their ability to quickly take advantage of them.
In other words, dumb luck was just that, it required no awareness on the person’s part, whereas “smart” luck involved awareness followed by action before the circumstances changed.
So, was I “lucky” to be born when I was—nothing I had any control over—and that I came of age just as huge databases and computers were advancing to the point where I could use those tools to write “What Works on Wall Street?” Absolutely.
Was I lucky to start my stock market investments near the peak of interest rates which allowed me to spend the majority of my adult life in a falling rate environment? Yup.
Ironies of Luck https://t.co/5BPWGbAxFi
— Morgan Housel (@morganhousel) March 14, 2018
"Luck is the flip side of risk. They are mirrored cousins, driven by the same thing: You are one person in a 7 billion player game, and the accidental impact of other people\u2019s actions can be more consequential than your own."
I’ve always felt that the luckiest people I know had a talent for recognizing circumstances, not of their own making, that were conducive to a favorable outcome and their ability to quickly take advantage of them.
In other words, dumb luck was just that, it required no awareness on the person’s part, whereas “smart” luck involved awareness followed by action before the circumstances changed.
So, was I “lucky” to be born when I was—nothing I had any control over—and that I came of age just as huge databases and computers were advancing to the point where I could use those tools to write “What Works on Wall Street?” Absolutely.
Was I lucky to start my stock market investments near the peak of interest rates which allowed me to spend the majority of my adult life in a falling rate environment? Yup.