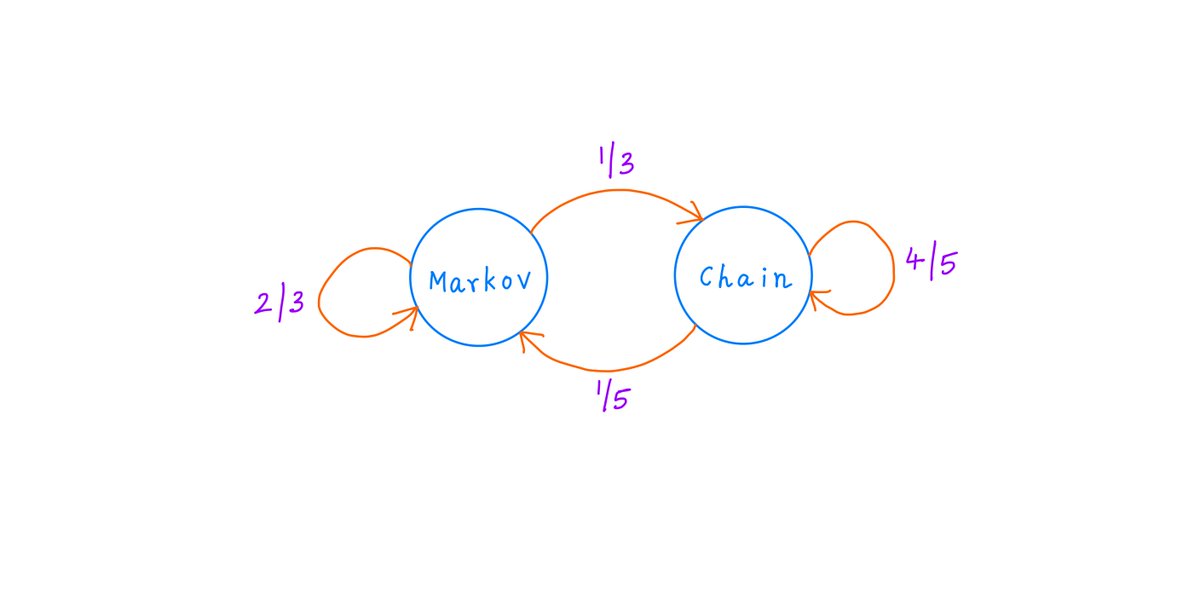
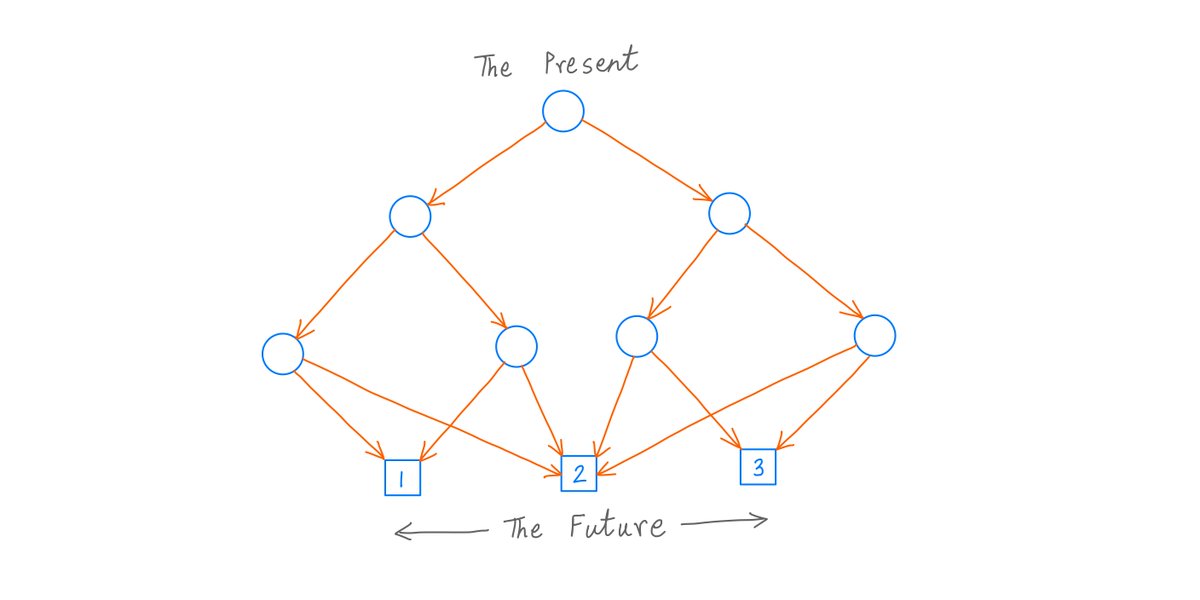
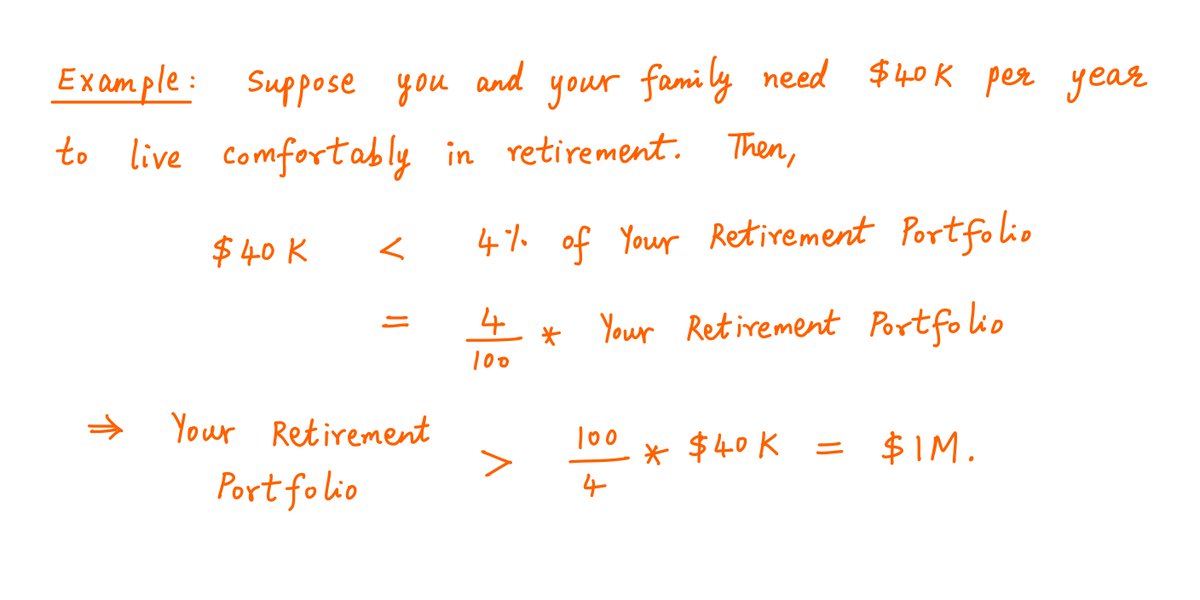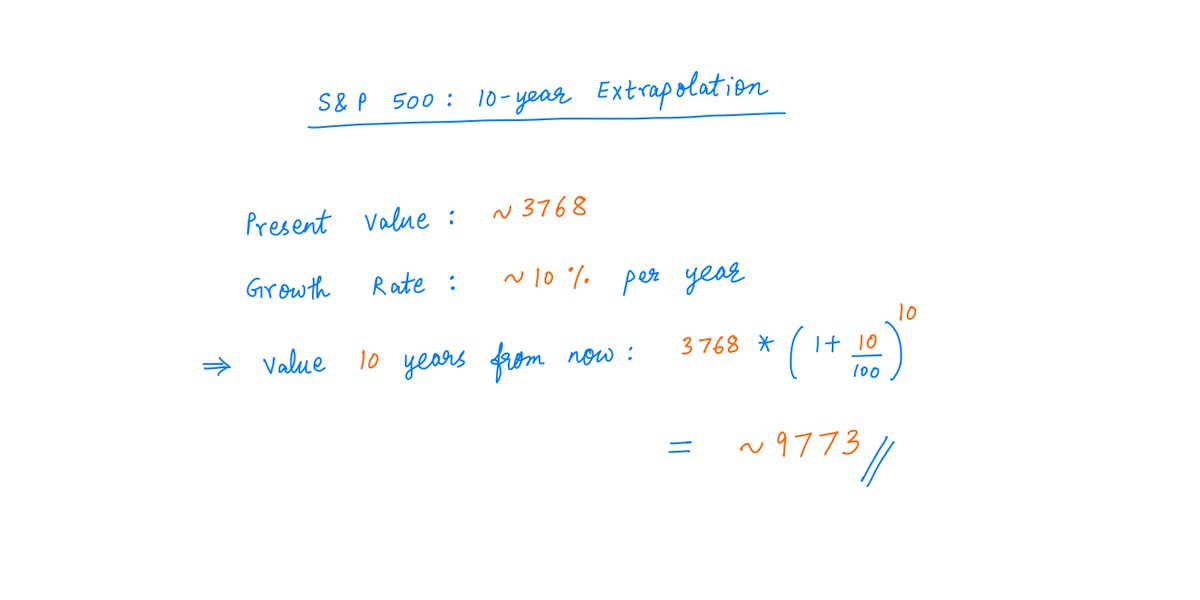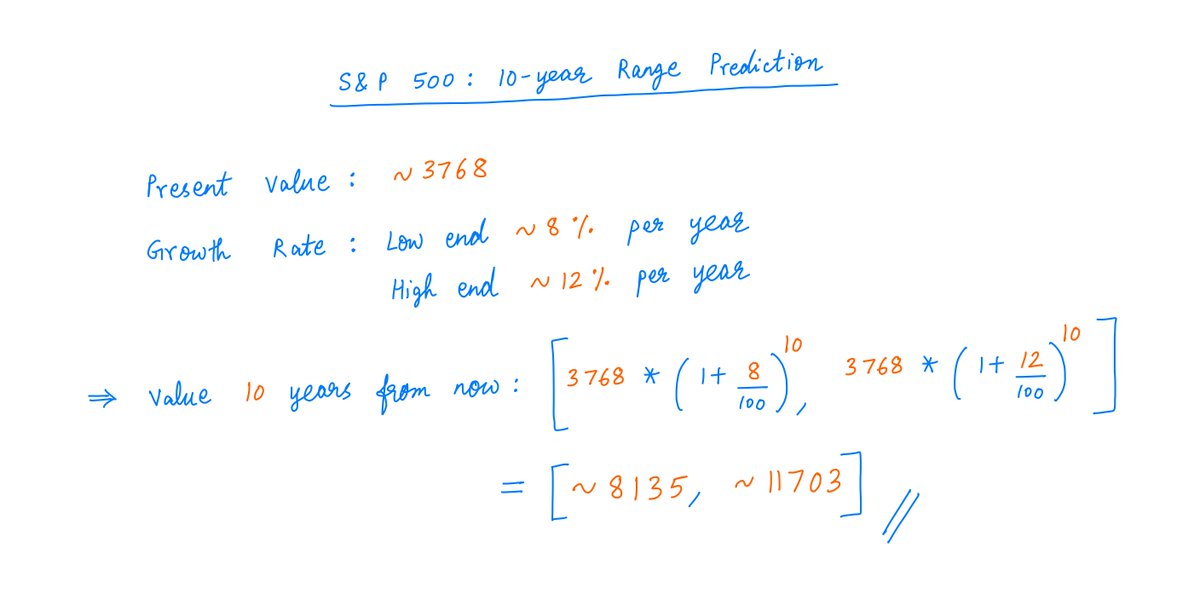Authors 10-K Diver
7 days
30 days
All time
Recent
Popular
1/
Get a cup of coffee.
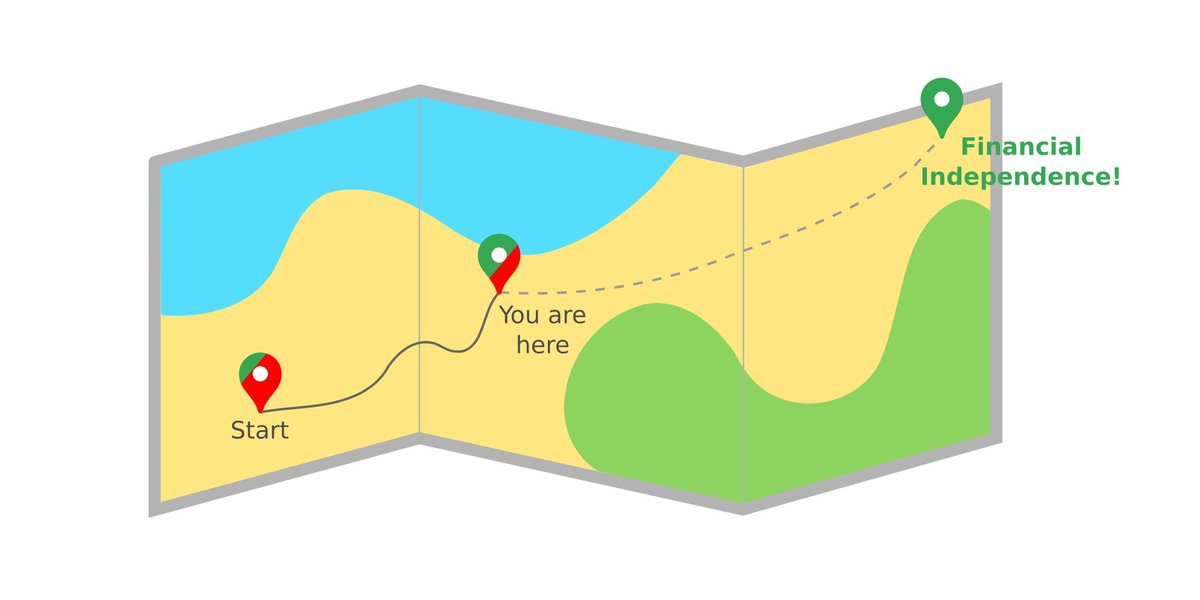
In this thread, I'd like to share with you a simple way to measure and track your progress towards financial independence.
2/
Financial independence is an end goal.
To define this goal properly, you need to answer 2 key questions.
(i) When would you consider yourself financially independent? And,
(ii) In how much time do you want to get there?
3/
Typically, financial independence means:
a) You won't have to work another day in your life for money, and
b) You and your family will still be able to live comfortably to the end of your days.
4/
Let's say you want to reach financial independence in the next 10 years.
How much money do you need to amass by that time?
Well, suppose your family's expenses are ~$60K per year now.
If inflation runs at ~2% per year, 10 years from now, your annual expenses will be ~$75K.
5/
Let's say you want your expenses to be under 3% of your portfolio at that time.
This is called the "3% Rule".
It means your portfolio's size should be about $2.5M (as 3% of $2.5M = $75K).
For more on the 3% Rule and such:
Get a cup of coffee.
In this thread, I'd like to share with you a simple way to measure and track your progress towards financial independence.

2/
Financial independence is an end goal.
To define this goal properly, you need to answer 2 key questions.
(i) When would you consider yourself financially independent? And,
(ii) In how much time do you want to get there?
3/
Typically, financial independence means:
a) You won't have to work another day in your life for money, and
b) You and your family will still be able to live comfortably to the end of your days.
4/
Let's say you want to reach financial independence in the next 10 years.
How much money do you need to amass by that time?
Well, suppose your family's expenses are ~$60K per year now.
If inflation runs at ~2% per year, 10 years from now, your annual expenses will be ~$75K.
5/
Let's say you want your expenses to be under 3% of your portfolio at that time.
This is called the "3% Rule".
It means your portfolio's size should be about $2.5M (as 3% of $2.5M = $75K).
For more on the 3% Rule and such:
1/
— 10-K Diver (@10kdiver) July 25, 2020
Get a cup of coffee.
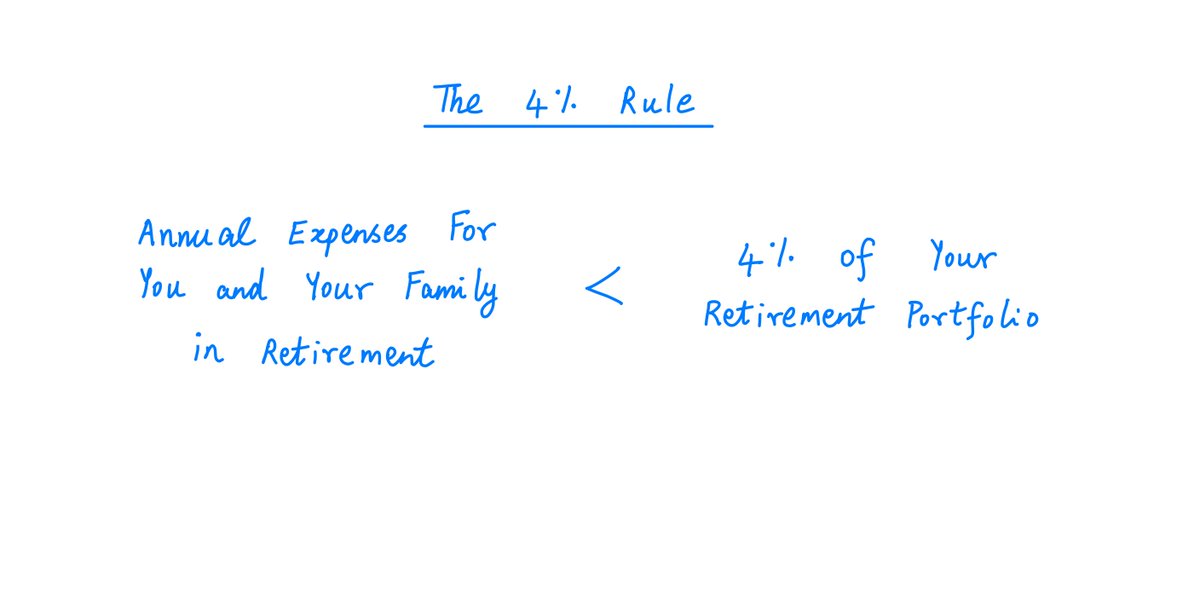
In this thread, I'll help you work out how much money you need to retire.
1/
Get a cup of coffee.
In this thread, let's talk snowballs.
Snowballs are super fun! And they can teach us so much about life, about things that grow over time, their rates of growth, compounding, etc.

2/
Snowballs are often used as a metaphor for compounding.
A snowball starts small at the top of a hill. As it rolls downhill, it picks up speed and grows in size. This is like money compounding over time.
For example, here's Buffett's famous "snowball quote":

3/
There's even a famous book about Buffett with "snowball" in the title.
The book's theme is similar to the quote above: the process of compounding is like a snowball that grows over time as it rolls downhill.
Link: https://t.co/L3opOrdeoZ

4/
Clearly, snowballs rolling downhill are worthy objects of study.
So let's dive into their physics!
Luckily for us, in 2019, Scott Rubin published a paper analyzing such snowballs -- in a journal called "The Physics Teacher".
All we need to do is understand this paper.

5/
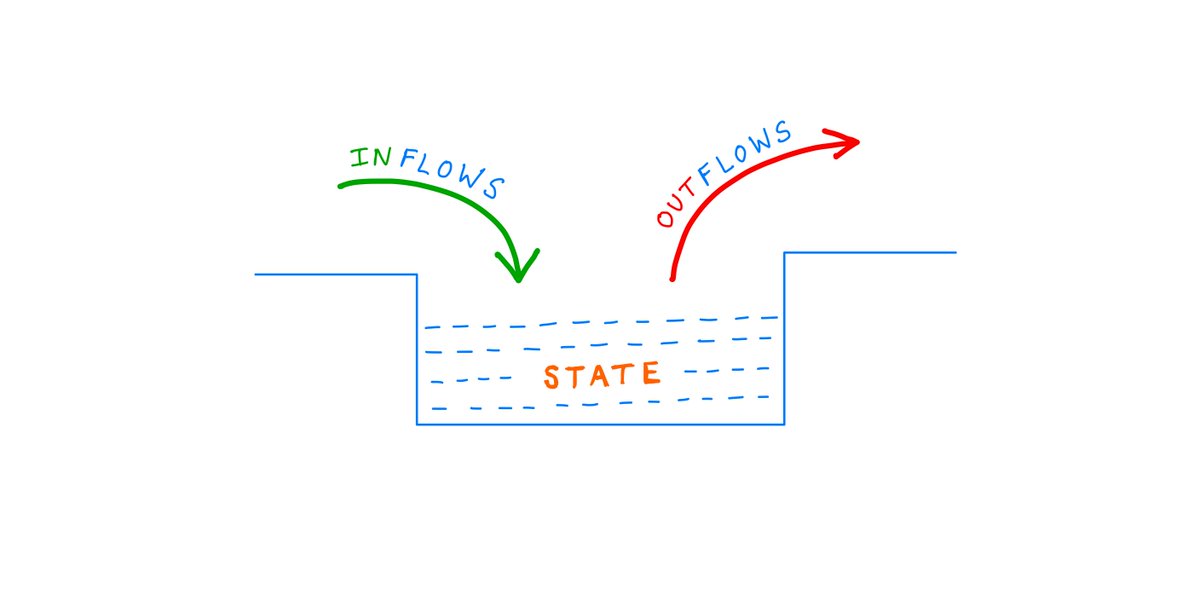
We begin by identifying 2 kinds of quantities in our "snowball system":
1. "Parameters" that don't change with time (eg, the hill's angle of incline), and
2. "State Variables" that *do* change with time (eg, the snowball's radius and velocity).

Get a cup of coffee.
In this thread, let's talk snowballs.
Snowballs are super fun! And they can teach us so much about life, about things that grow over time, their rates of growth, compounding, etc.

2/
Snowballs are often used as a metaphor for compounding.
A snowball starts small at the top of a hill. As it rolls downhill, it picks up speed and grows in size. This is like money compounding over time.
For example, here's Buffett's famous "snowball quote":

3/
There's even a famous book about Buffett with "snowball" in the title.
The book's theme is similar to the quote above: the process of compounding is like a snowball that grows over time as it rolls downhill.
Link: https://t.co/L3opOrdeoZ

4/
Clearly, snowballs rolling downhill are worthy objects of study.
So let's dive into their physics!
Luckily for us, in 2019, Scott Rubin published a paper analyzing such snowballs -- in a journal called "The Physics Teacher".
All we need to do is understand this paper.

5/
We begin by identifying 2 kinds of quantities in our "snowball system":
1. "Parameters" that don't change with time (eg, the hill's angle of incline), and
2. "State Variables" that *do* change with time (eg, the snowball's radius and velocity).

1/
Get a cup of coffee.
In this thread, I'll walk you through 2 probability concepts: Standard Deviation (SD) and Mean Absolute Deviation (MAD).
This will give you insight into Fat Tails -- which are super useful in investing and in many other fields.
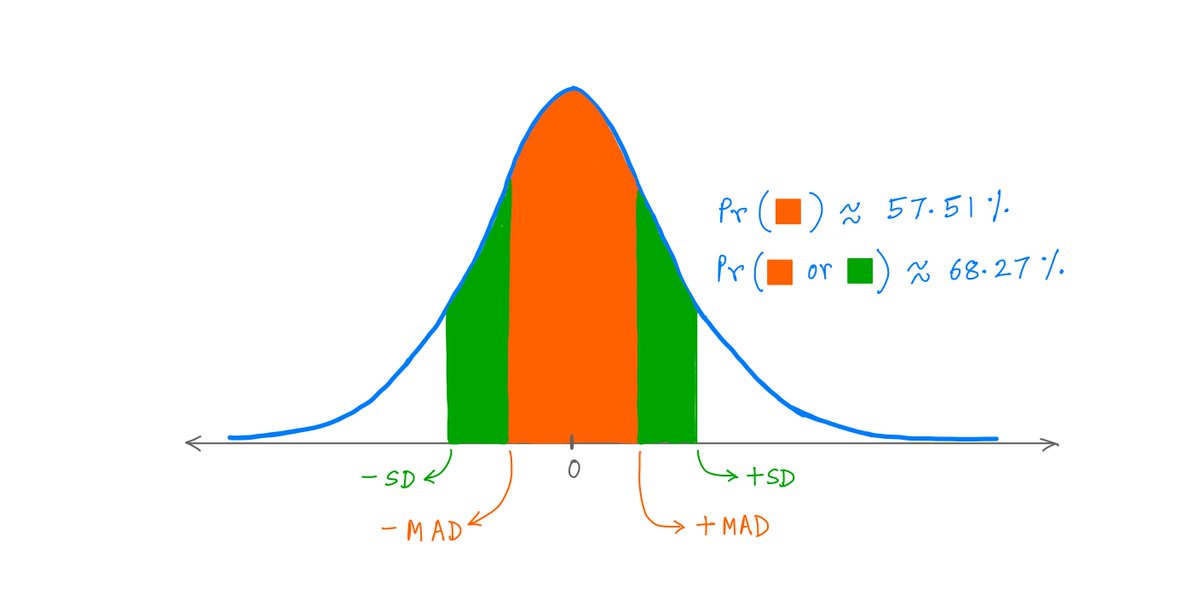
2/
Recently, I watched 2 probability "mini-lectures" on YouTube by Nassim Taleb.
One ~10 min lecture covered SD and MAD. The other ~6 min lecture covered Fat Tails.
In these ~16 mins, @nntaleb shared so many useful nuggets that I had to write this thread to unpack them.
3/
For those curious, here are the YouTube links to the lectures:
SD and MAD (~10 min): https://t.co/0TwubymdE6
Fat Tails (~6 min):
4/
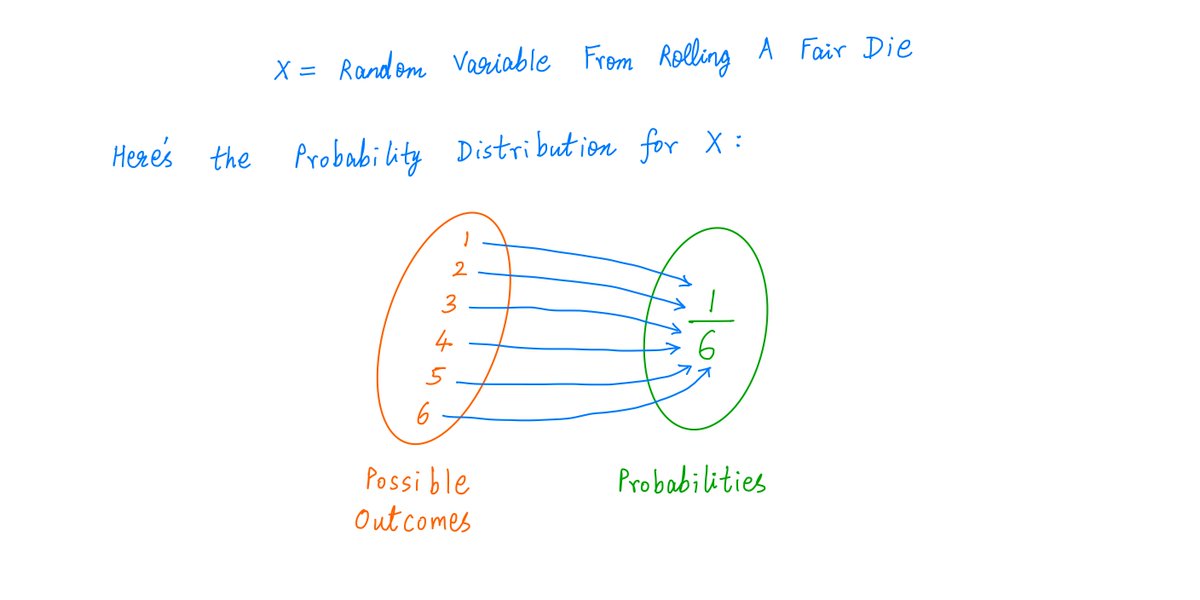
The first thing to understand is the concept of a Random Variable.
In essence, a Random Variable is a number that depends on a random event.
For example, when we roll a die, we get a Random Variable -- a number from the set {1, 2, 3, 4, 5, 6}.
5/
Every Random Variable has a Probability Distribution.
This tells us all the possible values the Random Variable can take, and their respective probabilities.
For example, when we roll a fair die, we get a Random Variable with this Probability Distribution:
Get a cup of coffee.
In this thread, I'll walk you through 2 probability concepts: Standard Deviation (SD) and Mean Absolute Deviation (MAD).
This will give you insight into Fat Tails -- which are super useful in investing and in many other fields.

2/
Recently, I watched 2 probability "mini-lectures" on YouTube by Nassim Taleb.
One ~10 min lecture covered SD and MAD. The other ~6 min lecture covered Fat Tails.
In these ~16 mins, @nntaleb shared so many useful nuggets that I had to write this thread to unpack them.
3/
For those curious, here are the YouTube links to the lectures:
SD and MAD (~10 min): https://t.co/0TwubymdE6
Fat Tails (~6 min):
4/
The first thing to understand is the concept of a Random Variable.
In essence, a Random Variable is a number that depends on a random event.
For example, when we roll a die, we get a Random Variable -- a number from the set {1, 2, 3, 4, 5, 6}.
5/
Every Random Variable has a Probability Distribution.
This tells us all the possible values the Random Variable can take, and their respective probabilities.
For example, when we roll a fair die, we get a Random Variable with this Probability Distribution: