The day has come. Enter a thread on isogenies, random walk…

I will explain some of the background we used to write these papers with Ben Smith, so I encourage you to go read them. There are some results at the end of the thread too!

https://t.co/ZvOjLWdxXY

(1/n)

My first two papers are out in the arXiv! I'm very thrilled about them \U0001f604 pic.twitter.com/Az9gODokH9
— Enric Florit (@enricflorit) January 5, 2021

The main objects in isogeny-based cryptography are elliptic curves and isogenies, usually defined over finite fields. And, of course, isogeny graphs.

(2/n)

You might want to read about elliptic curves here.

https://t.co/XHxOEuJMDN

(3/n)

\U0001f369 elliptic curves thread \U0001f369

Disclaimer: this thread is not meant to be technical but rather a bunch of facts I find beautiful about elliptic curves. I hope you can find them beautiful as well.
If you want to learn more about this, read Silverman's Arithmetic of Elliptic Curves!
— \u2133 \u2606\xb0\u30df (@computer_dream) December 31, 2020

First of all, an isogeny is a nonconstant morphism of elliptic curves fixing the point at infinity.

So it is a group morphism, a morphism of algebraic curves, it is surjective, and it has finite kernel.

https://t.co/WWSDCbtavl

(4/n)

The size of the kernel is the degree of the isogeny (whenever it is coprime to the characteristic of the finite field).

(5/n)

Isogenies can be thought of as "quotienting out" your curve by the kernel. Another useful concept to keep in mind is that of the dual.

(6/n)

Given an isogeny

a:E1→E2

of degree n, there is a dual isogeny

â:E2→E1,

such that the composition of both is the multiplication-by-n endomorphism.

(7/n)

So, the dual is almost an inverse, but when you get back you carry the degree. Isogenies of degree 1 are isomorphisms.

(8/n)

The supersingular isogeny graph is the graph of (isomorphism classes of) supersingular elliptic curves and the isogenies between them. They can be thought of as undirected graphs (more on that later).

(9/n)

You might know SIDH, which works with supersingular elliptic curves and low-degree isogenies.

(for instance, the previous graph, which consists of degree-2 and 3 isogenies)

https://t.co/qZx1hVEEya

(10/n)

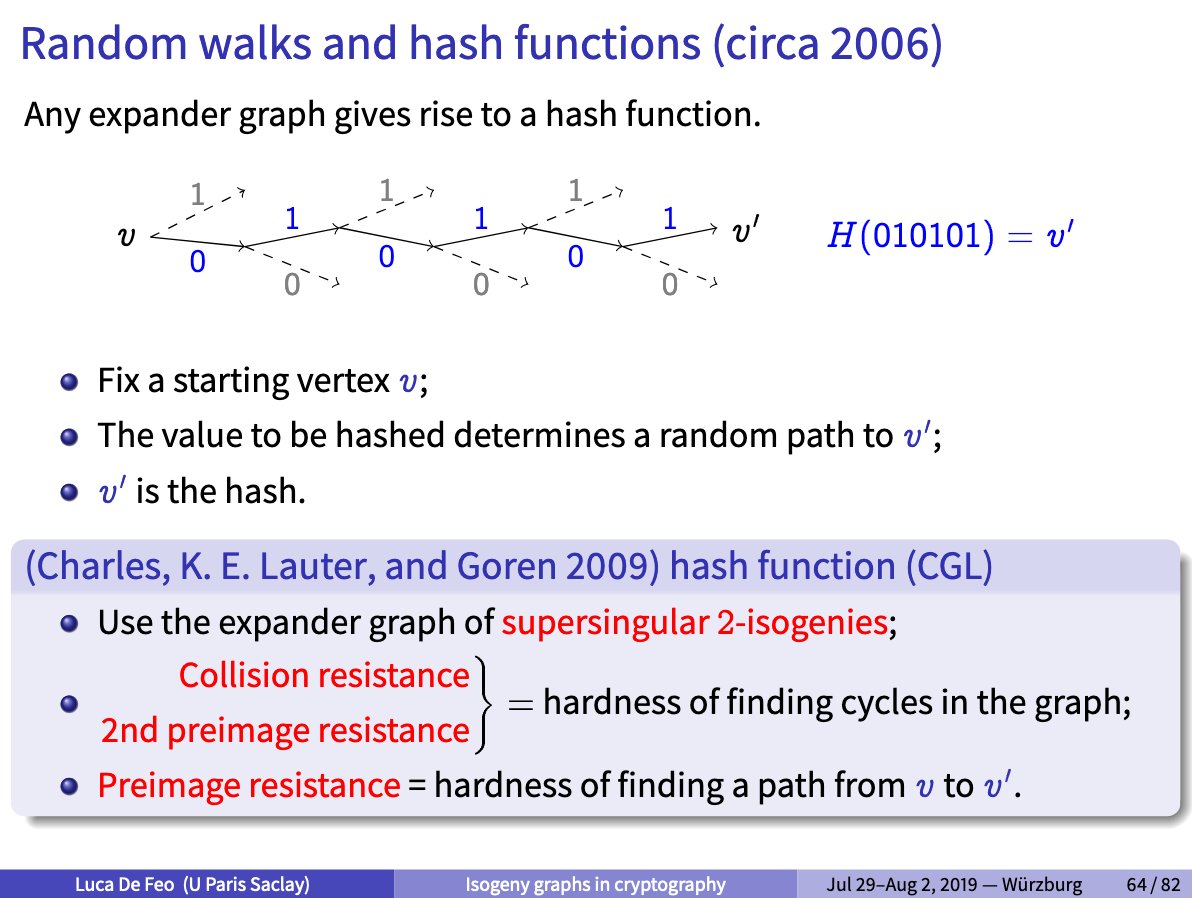
You might also know the Charles-Goren-Lauter hash function, which did actually come first.

https://t.co/Uj8isRiGnC

(11/n)

This hash function is easy to describe: a sequence of bits determines a random walk in the 2-isogeny graph, which is a 3-regular graph.

(slide from https://t.co/gbHPME4w8D)

(12/n)

The walk is determined because we avoid backtracking, so only 2 path choices are actually available at each step.

(13/n)

Let's talk a bit about random walks on graphs. They are a kind of discrete-time finite Markov chain. This means that at any time (natural time, t=0,1,2...) you are in one of finitely many states, in this case, nodes.

https://t.co/yEzgyk3nYu

(14/n)

The probability that you go from one node to the next is (essentially) 1/{degree of current node}. What happens if you have multiple edges, or weights? {weight from A to B}/{total weight from A}.

(15/n)

If your graph is acyclic and connected, there is a distribution on the set nodes that you will converge to, no matter where you start.

(16/n)

Eventually, if you start on any vertex, you'll have a well-defined stable probability to be in any other given vertex.

https://t.co/McytreYG69

(17/n)

The rate to which you converge to this stationary distribution is governed by the second eigenvalue of the random walk transition matrix (or adjacency matrix, if the graph happens to be regular).

(18/n)

We need a definition: a family of expander graphs is just a collection of (growing) d-regular graphs with uniformly bounded eigenvalues.

https://t.co/D15Au2xt5n

(19/n)

Moreover, if the second eigenvalue is as small as theoretically possible, we say the graphs are Ramanujan.

https://t.co/06kAukbFa1

(20/n)

How awesome is it that isogeny graphs are Ramanujan? Very awesome. That's one of the reasons we like them so much. It is a highly non-trivial fact that comes from the Weil conjectures (more on that another day. maybe)

https://t.co/hyx2UZ6Bbc

(21/n)

There is a catch in the case of supersingular isogeny graphs: when you take one such graph in characteristic p != 1 mod 12, the graph stops being undirected.

(22/n)

The behaviour is a bit strange, so I hope this picture helps. Essentially, there are two nodes where the number of out-going edges is the same as in the rest of the graph... but the number of incoming ones changes.

(23/n)

If you look at why (something you might do when learning SIDH, for instance), it is because these curves have more automorphisms than usual. Remember this.

(24/n)

However, this doesn't bother us, since it is _just_ 2 nodes out of p/12. It is a negligible effect, even in terms of Ramanujan-ness. For example, the primes used in SIDH are congruent to 11 mod 12.

(25/n)

It does change the stationary distribution I talked about, BUT (and this is extremely important) the probability of landing in any other curve is exactly the same.

(26/n)

The stationary distribution is constant outside the "bad nodes".

(27/n)

Is everything done for elliptic curve isogenies? Not at all!
Just to name a couple of open questions: (1) we are not sure about the fastest way to compute an isogeny, and

(28/n)

(2) we don't know how to produce a random curve while guaranteeing no one (including us) knows its endomorphism ring.

(29/n)

But still, people have been asking: what happens when you go higher genus?

There are a number of challenges, but the most important one is that computing isogenies is not that easy. It isn't even implemented in Sage.

(30/n)

It is in Magma (https://t.co/dmAcxcRZZG), but I haven't tried that myself. I hear there is a lot of algebraic geometry going on in the theoretical part of it (personal todo/reading list).

(31/n)

But what _is_ an isogeny in higher genus?

For what is worth, what _are_ the analogues of elliptic curves?

(32/n)

The answer is (are) principally polarized abelian varieties, or PPAVs to abbrviate.

There are two classes of them: jacobians of curves, and products of lower-dimensional PPAVs. Let's talk about genus two.

(33/n)

Curves of genus two can be given by nonsingular hyperelliptic equations y^2 = ax^6 + ... (there is an issue with just going projective with this, but it is solved by using weighted coordinates)

https://t.co/Nf8eCjlmhw

(34/n)

The jacobians of such curves are two-dimensional abelian varieties, or surfaces (PPASs).

(35/n)

Product varieties in dimension 2 are easy: just take products of elliptic curves!

(36/n)

There is a definition of supersingular in higher dimension, but the proper analogue here is _superspecial_ (a stronger notion).

https://t.co/wdmIa6oxcg

(37/n)

In practice, this means that all the elliptic curves appearing in products in our graph are supersingular. But please do not take this as a definition.

(38/n)

Isogenies, as before, are nonconstant maps between PPAS that fix the zero, are surjective, and have finite kernel (and that are compatible with the polarization).

(39/n)

An isogeny between E1xE2 and E3xE4 (E1, E2, E3, E4 being elliptic curves) is just the product of two isogenies a:E1→E2 and b:E3→E4.

If r=deg(a), and s=deg(b), we say a x b is an (r,s)-isogeny.

(40/n)

The pair (r,s) essentially tells the group structure of the kernel (I'm always assuming degrees and characteristic have no relation, i.e. they are coprime).

(41/n)

The kernel structure part is more important than the fact that some isogenies are products.

There are isogenies between abelian surfaces of type (4,4,2), for instance.

(42/n)

Isogenies between elliptic products are easy, what about jacobians? We have to take a look at Richelot isogenies.

(43/n)

Given the hyperelliptic curve C: y^2 = f(x), with deg f = 6, we take a quadratic splitting f(x) = g1(x)g2(x)g3(x) (there are 15 ways to do that).

The Richelot isogeny gives a curve D: y^2 = h(x).

(44/n)

The Jacobians of C and D are related by a (2,2)-isogeny Jac(C)→Jac(D).

Sometimes this fails a little bit (something quite curious arithmetically), and it degenerates into an isogeny Jac(C)→E1xE2.

(45/n)

All these isogenies have duals, as you'd expect.

But! Two isogenies can share the same dual. A picture is worth several thousand words here (numbers are isogeny counts). Isn't it beautiful?

(46/n)

What's causing these imbalances?

As in the genus 1 case, the answer is automorphisms. If an automorphism fixes the kernel of an isogeny, that's fine, but if it changes it, it gives a different isogeny.

(47/n)

However, these two isogenies are now _isomorphic_, and they'll probably have the same dual. Unless the same thing happens in the codomain variety, of course.

(48/n)

What we have to look at is both the automorphism group of both varieties, AND the stabilizers of the kernels.

(49/n)

Katsura and Takashima looked at this about a year ago: https://t.co/i527jnk0sh

(50/n)

Nicely enough, the stabilizer of the kernel of an isogeny is isomorphic to the stabilizer of the kernel of the dual.

That is Lemma 1 in https://t.co/wsXTvNCfLA

(51/n)

This restricts the kinds of nodes that can be neighbors. For instance, a jacobian with only two automorphisms ([1] and [-1]) cannot have a (2,2)-isogeny to an elliptic product, which always has more automorphisms.

(52/n)

Okay, what happens next is quite surprising: the number of PPASs with extra automorphisms actually _grows_ with p. The proportion in the entire graph is 1/p, which is less than negligible.

(53/n)

This makes the graph a directed one, by the way! We have quite good control on undirected graphs and random walks (see here https://t.co/ySamXQczdA), but directed graphs are a whole other world.

(54/n)

This changes the stationary distribution of the random walk on these graphs. Luckily, though, one is able to control it. The reason lies very close to the adjoint property of Hecke operators.

(55/n)

And the distribution is constant on each set of varieties with the same automorphism group, so it is not so bad.

(56/n)

So, are higher-genus isogenies still good for, say, hash functions?

(57/n)

This has already been done (twice), and it has already a nontrivial answer if one wants to avoid trivial collisions. But it is doable. If you are curious, it hashes three bits per random walk step.

(58/n)

Katsura's paper on this https://t.co/CptrFlArBQ

(59/n)

Castryck-Decru-Smith's paper on this
https://t.co/VwA1siu9SP

(60/n)

However, the distribution of the hash is not uniform in the set of possible outcomes. Is it that bad? I'd say no, since one can always increase the size of the prime, but it is important to keep it in mind.

(61/n)

Actually, the proposed algorithm for hashing in genus two still has to solve some other issues (what happens if the random walk ends in an elliptic product?)

(62/n)

Back to our random walks, we don't have the Ramanujan property for g=2 and (2,2)-isogenies. We conjecture the eigenvalues should remain bounded, though.

(63/n)

This would prove, for instance, that the graph diameter grows as log(p).

(64/n)

I will be ending here, since this thread is already way too long. I shall expand on a few of these things in the future!

(65/n)

I hope you have liked it 😇😄

(66/n, n=66)

The day has come.

Enter a thread on isogenies, random walks and automorphism groups.

🧵👇

(0/n)

More from Science

You May Also Like

The day has come.Enter a thread on isogenies, random walks and automorphism groups.🧵👇(0/n)

More from Science

You May Also Like

The day has come.

Enter a thread on isogenies, random walks and automorphism groups.

🧵👇

(0/n)